题目内容
3.若不等式x2+y2≤2所表示的区域为M,不等式组$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{y≥2x-6}\end{array}\right.$表示的平面区域为N,现随机向区域N内抛一粒豆子,则豆子落在区域M内的概率为$\frac{π}{24}$.分析 由题意,所求概率满足几何概型的概率,只要分别求出S阴影,SN,求面积比即可.
解答 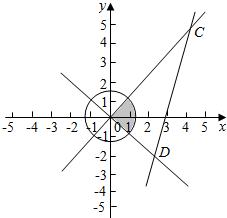 解:由题,图中△OCD表示N区域,其中C(6,6),D(2,-2)
解:由题,图中△OCD表示N区域,其中C(6,6),D(2,-2)
所以SN=$\frac{1}{2}$×$6\sqrt{2}×2\sqrt{2}$=12,S阴影=$\frac{2π}{4}$=$\frac{π}{2}$,
所以豆子落在区域M内的概率为$\frac{π}{24}$.
故答案为:$\frac{π}{24}$.
点评 本题主要考查了几何概率的求解,以及线性规划的知识,属于简单综合.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
18.如图,在正方体ABCD-A1B1C1D1中,若M是线段A1C1上的动点,则下列结论不正确的是( )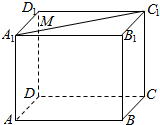

| A. | 三棱锥M-ABD的主视图面积不变 | B. | 三棱锥M-ABD的侧视图面积不变 | ||
| C. | 异面直线CM,BD所成的角恒为$\frac{π}{2}$ | D. | 异面直线CM,AB所成的角可为$\frac{π}{4}$ |
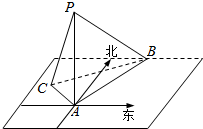 如图所示,在海岛A上有一座海拔$\sqrt{3}$千米的山峰上,山顶上设有一座观察站P,一艘轮船沿一固定方向匀速航行,上午10:00时,测得此船在岛北偏东20°且俯角为30°的B处,到10:10时,又测得该船在岛北偏西40°且俯角为60°的C处,则该船的航行速度为$6\sqrt{7}$千米/时.
如图所示,在海岛A上有一座海拔$\sqrt{3}$千米的山峰上,山顶上设有一座观察站P,一艘轮船沿一固定方向匀速航行,上午10:00时,测得此船在岛北偏东20°且俯角为30°的B处,到10:10时,又测得该船在岛北偏西40°且俯角为60°的C处,则该船的航行速度为$6\sqrt{7}$千米/时.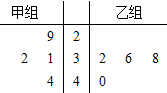 某商场为推销当地的某种特产进行了一次促销活动,将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销,每个小组各4人.以下茎叶图记录了这两个小组成员促销这种特产的件数.
某商场为推销当地的某种特产进行了一次促销活动,将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销,每个小组各4人.以下茎叶图记录了这两个小组成员促销这种特产的件数.