题目内容
用计算机随机产生的有序二元数组（x，y），满足-1＜x＜1，-1＜y＜1，对每一个二元数组（x，y），用计算机计算x2+y2的值，记A为事件“x2+y2＞1”，则事件A发生的概率是分析：本题是一个几何概型，试验发生包含的事件对应的集合是Ω={（x，y）|-1＜x＜1，-1＜y＜1}，满足条件的事件对应的集合是A={（x，y）|-1＜x＜1，-1＜y＜1，x2+y2＞1}，做出两个集合对应的图形的面积，根据几何概型概率公式得到结果．
解答：解：由题意知本题是一个几何概型，
试验发生包含的事件对应的集合是Ω={（x，y）|-1＜x＜1，-1＜y＜1}，
它的面积是2×2=4，
满足条件的事件对应的集合是A={（x，y）|-1＜x＜1，-1＜y＜1，x2+y2＞1}
集合A对应的图形的面积是边长为2的正方形内部，且圆的外部，面积是4-π
∴根据几何概型的概率公式得到P=
故答案为：
试验发生包含的事件对应的集合是Ω={（x，y）|-1＜x＜1，-1＜y＜1}，
它的面积是2×2=4，
满足条件的事件对应的集合是A={（x，y）|-1＜x＜1，-1＜y＜1，x2+y2＞1}
集合A对应的图形的面积是边长为2的正方形内部，且圆的外部，面积是4-π
∴根据几何概型的概率公式得到P=
| 4-π |
| 4 |
故答案为：
| 4-π |
| 4 |
点评：本题是一个几何概型，对于这样的问题，一般要通过把试验发生包含的事件同集合结合起来，根据集合对应的图形做出面积，用面积的比值得到结果．
练习册系列答案
春雨教育同步作文系列答案
相关题目
，现用随机模拟的方法估计y=f（x）与x=4及x轴围成的面积S，用计算机先产生两组（每组30个）在区间[0，4]上的均匀随机数x1，x2，…，x30和y1，y2，…，y30，由此得到30个点（xi，yi）（i=1，2，…，30），现数出其中满足yi≤f（xi）（i=1，2，…，30）的点有10个，则由随机模拟的方法可估计得到面积S为（ ）
，现用随机模拟的方法估计y=f（x）与x=4及x轴围成的面积S，用计算机先产生两组（每组30个）在区间[0，4]上的均匀随机数x1，x2，…，x30和y1，y2，…，y30，由此得到30个点（xi，yi）（i=1，2，…，30），现数出其中满足yi≤f（xi）（i=1，2，…，30）的点有10个，则由随机模拟的方法可估计得到面积S为（ ）
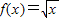，现用随机模拟的方法估计y=f（x）与x=4及x轴围成的面积S，用计算机先产生两组（每组30个）在区间[0，4]上的均匀随机数x1，x2，…，x30和y1，y2，…，y30，由此得到30个点（xi，yi）（i=1，2，…，30），现数出其中满足yi≤f（xi）（i=1，2，…，30）的点有10个，则由随机模拟的方法可估计得到面积S为（ ）
