题目内容
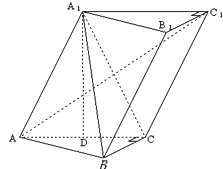 在三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.
在三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.(1)求证:AC1⊥平面A1BC;
(2)求二面角A1-BC-A的大小;
(3)求CC1到平面A1AB的距离.
分析:(1)欲证AC1⊥平面A1BC,根据直线与平面垂直的判定定理可知只需证AC1与平面A1BC内两相交直线垂直,利用平面和平面垂直的性质定理可以证出BC⊥AC1,又BA1⊥AC1,满足定理条件;
(2)在证得BC⊥平面AA1C1C的基础上,可以知道∠A1CA为面角A1-BC-A的平面角,通过证明△A1CA为正三角形得出∠A1CA=60°
(3)取AA1中点F,则AA1⊥平面BCF,从而面A1AB⊥面BCF,过C作CH⊥BF于H,则CH⊥面A1AB,从而CH就是CC1到平面A1AB的距离,在Rt△BCF中,求出CH即可
(2)在证得BC⊥平面AA1C1C的基础上,可以知道∠A1CA为面角A1-BC-A的平面角,通过证明△A1CA为正三角形得出∠A1CA=60°
(3)取AA1中点F,则AA1⊥平面BCF,从而面A1AB⊥面BCF,过C作CH⊥BF于H,则CH⊥面A1AB,从而CH就是CC1到平面A1AB的距离,在Rt△BCF中,求出CH即可
解答: (1)证明:因为A1D⊥平面ABC,所以平面AA1C1C⊥平面ABC,
(1)证明:因为A1D⊥平面ABC,所以平面AA1C1C⊥平面ABC,
又BC⊥AC,所以BC⊥平面AA1C1C,
得BC⊥AC1,又BA1⊥AC1
所以AC1⊥平面A1BC;(4分)
(2)解:由(1)已证BC⊥平面AA1C1C,所以BC⊥AC,BC⊥A1C,∠A1CA为二面角A1-BC-A的平面角.
由AC1⊥平面A1BC,得出AC1⊥A1C,所以平行四边形AA1C1C为菱形.
由于A1在底面ABC上的射影恰为AC的中点D,所以A1A=A1C,所以△A1CA为正三角形,得出∠A1CA=60°
即二面角A1-BC-A的大小为60°
(3)解:由(2)四边形AA1C1C为菱形,△A1CA为正三角形,
故AA1=AC=2,∠A1AC=60°.
取AA1中点F,则AA1⊥CF又 AA1⊥BC,所以AA1⊥平面BCF,从而面A1AB⊥面BCF,
过C作CH⊥BF于H,则CH⊥面A1AB,
在Rt△BCF中,BC=2,CF=
,故CH=
,
即CC1到平面A1AB的距离为CH=
 (1)证明:因为A1D⊥平面ABC,所以平面AA1C1C⊥平面ABC,
(1)证明:因为A1D⊥平面ABC,所以平面AA1C1C⊥平面ABC,又BC⊥AC,所以BC⊥平面AA1C1C,
得BC⊥AC1,又BA1⊥AC1
所以AC1⊥平面A1BC;(4分)
(2)解:由(1)已证BC⊥平面AA1C1C,所以BC⊥AC,BC⊥A1C,∠A1CA为二面角A1-BC-A的平面角.
由AC1⊥平面A1BC,得出AC1⊥A1C,所以平行四边形AA1C1C为菱形.
由于A1在底面ABC上的射影恰为AC的中点D,所以A1A=A1C,所以△A1CA为正三角形,得出∠A1CA=60°
即二面角A1-BC-A的大小为60°
(3)解:由(2)四边形AA1C1C为菱形,△A1CA为正三角形,
故AA1=AC=2,∠A1AC=60°.
取AA1中点F,则AA1⊥CF又 AA1⊥BC,所以AA1⊥平面BCF,从而面A1AB⊥面BCF,
过C作CH⊥BF于H,则CH⊥面A1AB,
在Rt△BCF中,BC=2,CF=
| 3 |
2
| ||
| 7 |
即CC1到平面A1AB的距离为CH=
2
| ||
| 7 |
点评:本题考查了直线与平面垂直的判定,二面角的平面角大小计算,线面之间距离的计算.考查空间想象能力、转化、运算能力和推理论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
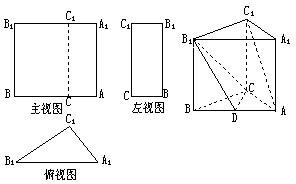 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5, 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.