题目内容
已知动直线?:y=kx+5和圆C(x-1)2+y2=1,试问k为何值时,直线?与⊙C相离?相切?相交?
分析:根据已知中圆的标准方程,我们可以分析出圆的圆心坐标和半径,结合直线的方程和点到直线距离公式,可又求出圆心到直线的距离d,进而根据直线与圆的位置关系的判定方法,可得直线?与⊙C相离,相切,相交时,k的取值范围.
解答:解:∵圆C(x-1)2+y2=1的圆心坐标为(1,0),半径为1
直线?:y=kx+5的方程可化为kx-y+5=0
则圆心C到直线?的距离d=
当d=
>1,即k>-
时,直线?与⊙C相离;
当d=
=1,即k=-
时,直线?与⊙C相切;
当d=
<1,即k<-
时,直线?与⊙C相交;
直线?:y=kx+5的方程可化为kx-y+5=0
则圆心C到直线?的距离d=
| |k+5| | ||
|
当d=
| |k+5| | ||
|
| 12 |
| 5 |
当d=
| |k+5| | ||
|
| 12 |
| 5 |
当d=
| |k+5| | ||
|
| 12 |
| 5 |
点评:本题考查的知识点是直线与圆的位置关系,熟练掌握直线与圆位置关系的判定方法及等价条件是解答的关键.

练习册系列答案
相关题目
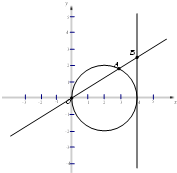 (2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足
(2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足