题目内容
设![]() ,函数
,函数![]() .
.
(1)若曲线![]() 在
在![]() 处切线的斜率为-1,求
处切线的斜率为-1,求![]() 的值;
的值;
(2)求函数![]() 的极值点
的极值点
(Ⅰ) ![]() (Ⅱ)当
(Ⅱ)当![]() 时,
时,![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点;当
的极小值点;当![]() 时,
时,![]() 没有极值点;当
没有极值点;当![]() 时,
时,![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点
的极小值点
解析:
(1)由已知![]() 2分
2分
![]() 4分
4分
曲线![]() 在
在![]() 处切线的斜率为-1,所以
处切线的斜率为-1,所以![]() 5分
5分
即![]() ,所以
,所以![]() 6分
6分
(2)![]() 8分
8分
①当![]() 时,
时,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增。
单调递增。
此时![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点 10分
的极小值点 10分
②当![]() 时,
时,
当![]() 时,
时,![]() >0,
>0,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
所以函数![]() 在定义域内单调递增,此时
在定义域内单调递增,此时![]() 没有极值点 11分
没有极值点 11分
③当![]() 时,[来源:]
时,[来源:]
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增
单调递增
此时![]() 是
是![]() 的极大值点,
的极大值点,
![]() 是
是![]() 的极小值点 13分
的极小值点 13分
综上,当![]() 时,
时,![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点;
的极小值点;
当![]() 时,
时,![]() 没有极值点;
没有极值点;
当![]() 时,
时,![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点
的极小值点

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
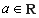

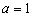
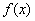
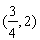
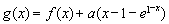
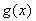
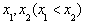
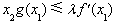
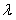
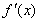
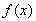
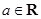 ,函数
,函数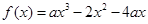 ,
, 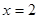 是函数
是函数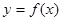 的极值点,求
的极值点,求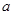 的值;
的值;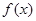 在区间
在区间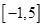 上的最值.
上的最值.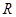 上为单调函数,若是,求出
上为单调函数,若是,求出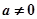 ,函数
,函数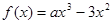 .
.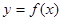 在
在 的最小值为-2,求a的值;
的最小值为-2,求a的值;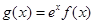 在
在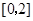 上是单调减函数,求实数
上是单调减函数,求实数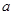 的取值范围.
的取值范围.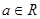 ,函数
,函数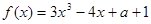 ,
, 的单调区间;
的单调区间;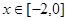 ,不等式
,不等式 恒成立,求
恒成立,求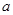 的取值范围。
的取值范围。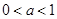 ,函数
,函数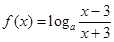 .
.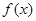 的定义域,并判断
的定义域,并判断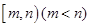 时,值域为
时,值域为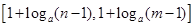 ,求
,求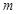 、
、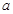 的取值范围.
的取值范围.