题目内容
设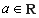 ,函数
,函数 .
.
(1)当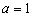 时,求
时,求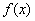 在
在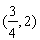 内的极大值;
内的极大值;
(2)设函数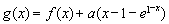 ,当
,当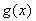 有两个极值点
有两个极值点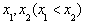 时,总有
时,总有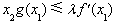 ,求实数
,求实数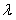 的值.(其中
的值.(其中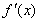 是
是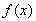 的导函数.)
的导函数.)
【答案】
(1)1;(2) 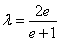 .
.
【解析】
试题分析:(1)当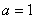 时,求
时,求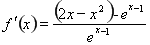 , 令
, 令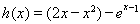 ,求
,求 ,利用
,利用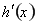 的单调性,求
的单调性,求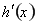 的最大值,利用
的最大值,利用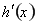 的最大值的正负,确定
的最大值的正负,确定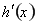 的正负,从而确定
的正负,从而确定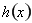 的单调性,并确定
的单调性,并确定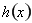 的正负,即
的正负,即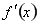 的正负,得到
的正负,得到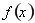 的单调性,确定极大值,此题确定极大值需要求二阶导数,偏难;(2)先求
的单调性,确定极大值,此题确定极大值需要求二阶导数,偏难;(2)先求 函数,再求
函数,再求 ,由方程
,由方程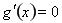 有两个不等实根
有两个不等实根 , 确定
, 确定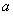 的范围,再将
的范围,再将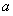 代入
代入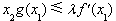 ,再整理不等式,讨论
,再整理不等式,讨论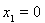 ,
,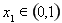 ,
,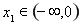 三种情况,反解
三种情况,反解 ,从而利于恒成立求出
,从而利于恒成立求出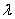 的范围.属于较难试题.
的范围.属于较难试题.
试题解析:(1)当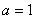 时,
时,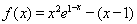 ,
,
则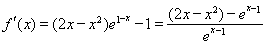 , 2分
, 2分
令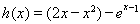 ,则
,则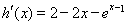 ,
,
显然 在
在 内是减函数,
内是减函数,
又因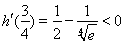 ,故在
,故在 内,总有
内,总有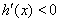 ,
,
所以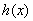 在
在 上是减函数 4分
上是减函数 4分
又因 , 5分
, 5分
所以当 时,
时, ,从而
,从而 ,这时
,这时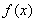 单调递增,
单调递增,
当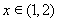 时,
时,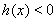 ,从而
,从而 ,这时
,这时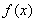 单调递减,
单调递减,
所以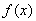 在
在 的极大值是
的极大值是 . 7分
. 7分
(2)由题可知 ,
,
则 . 8分
. 8分
根据题意,方程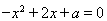 有两个不同的实根
有两个不同的实根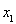 ,
,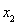 (
(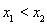 ),
),
所以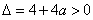 ,即
,即 ,且
,且 ,因为
,因为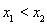 ,所以
,所以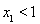 .
.
由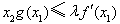 ,其中
,其中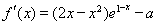 ,可得
,可得
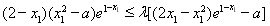
注意到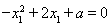 ,
,
所以上式化为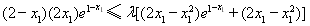 ,
,
即不等式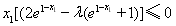 对任意的
对任意的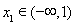 恒成立 10分
恒成立 10分
(i)当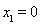 时,不等式
时,不等式 恒成立,
恒成立,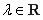 ;
;
(ii)当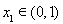 时,
时, 恒成立,即
恒成立,即 .
.
令函数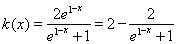 ,显然,
,显然,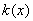 是
是 上的减函数,
上的减函数,
所以当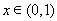 时,
时, ,所以
,所以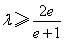 ; 12分
; 12分
(iii)当 时,
时, 恒成立,即
恒成立,即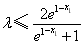 .
.
由(ii),当 时,
时,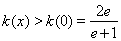 ,所以
,所以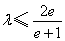 14分
14分
综上所述,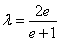 . 15分
. 15分
考点:1.利于导数求函数的极值;2.利用导数解决恒成立问题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 为实数,函数
为实数,函数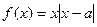 ,
,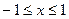 时,讨论
时,讨论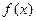 的奇偶性;
的奇偶性;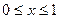 时,求
时,求 。
。 时,求函数
时,求函数 的定义域;
的定义域; ,试求
,试求 的取值范围.
的取值范围.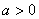 ,函数
,函数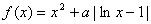 .
.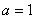 时,求曲线
时,求曲线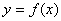 在点
在点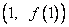 处的切线方程;
处的切线方程;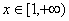 时,求函数
时,求函数 的最小值.
的最小值.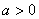 ,函数
,函数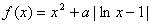 .
.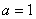 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,求函数
时,求函数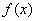 的最小值.
的最小值.