题目内容
已知正三角形OAB的三个顶点都在抛物线y2=2x上，其中O为坐标原点，设圆C是△OAB的外接圆(点C为圆心)．(1)求圆C的方程；
(2)设圆M的方程为(x
)2+(y
)2=1，过圆M上任意一点P分别作圆C的两条切线PE，PF，切点为E，F，求
的最大值和最小值．
答案：(1)由于O为原点，三角形OAB是正三角形，A，B两点在抛物线上，故A，B两点关于x轴对称，可知直线OA的倾角为，OA方程是y=x，代入y2=2x，解得A点坐标是A(6，)或A(6，
)同样可求得B点的坐标是B(6，
)或8(6，
)．
设圆心C的坐标为(r，O)，则r=
×6=4，
所以圆C的方程为：(x-4)4+y2=16．
(2)设∠ECF=2α，则
·cos2α=16cos2α=32cos2α-16．
在Rt△PCE中，cosα=
，M点的坐标是
，|MC|=7
|PC|≤|MC|+1=7+1=8．
|PC|≥|MC|-1=7-1=6．
所以
≤cosα≤
，由此可得-8≤
≤
．
则
的最大值为
，最小值为-8．
练习册系列答案
相关题目
上，其中O为坐标原点，设圆C是
的外接圆（点C为圆心）（1）求圆C的方程；（2）设圆M的方程为
，过圆M上任意一点P分别作圆C的两条切线PE、PF，切点为E、F，求
的最大值和最小值
的最大值和最小值．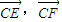
的最大值和最小值．