题目内容
已知正三角形OAB的三个顶点都在抛物线y2=2x上,其中O为坐标原点,设圆C是OAB的内接圆(点C为圆心)(I)求圆C的方程;
(II)设圆M的方程为(x-4-7cosθ)2+(y-7cosθ)2=1,过圆M上任意一点P分别作圆C的两条切线PE,PF,切点为E,F,求
 的最大值和最小值.
的最大值和最小值.
【答案】分析:(I)设出A、B的坐标(正三角形OAB的三个顶点都在抛物线y2=2x上),根据△ABO边长相等,求出A、B点的坐标,再求圆心和半径,进而求可得圆C的方程;
(II)设出∠ECF=2α,表示出数量积,数量积中有cosα, ,确定|PC|的范围,可求出数量积的最值.
,确定|PC|的范围,可求出数量积的最值.
解答:解:(I)解法一:设A,B两点坐标分别为 ,
, ,
,
由题设知
解得y12=y22=12,
所以 ,
, 或
或 ,
, .
.
设圆心C的坐标为(r,0),则 ,
,
所以圆C的方程为(x-4)2+y2=16.
解法二:设A,B两点坐标分别为(x1,y1),(x2,y2),由题设知x12+y12=x22+y22
又因为y12=2x1,y22=2x2,可得x12+2x1=x22+2x2.即(x1-x2)(x1+x2+2)=0
由x1>0,x2>0,可知x1=x2,故A,B两点关于x轴对称,所以圆心C在x轴上
设C点的坐标为(r,0),则A点坐标为 ,于是有
,于是有 ,
,
解得r=4,
所以圆C的方程为(x-4)2+y2=16.
(II)解:设∠ECF=2α,则 .
.
在Rt△PCE中, ,由圆的几何性质得|PC|≤|MC|+1=7+1=8,|PC|≥|MC|-1=7-1=6,
,由圆的几何性质得|PC|≤|MC|+1=7+1=8,|PC|≥|MC|-1=7-1=6,
所以 ,由此可得
,由此可得 .
.
则 的最大值为
的最大值为 ,最小值为-8.
,最小值为-8.
点评:本小题主要考查平面向量,圆与抛物线的方程及几何性质等基本知识,考查综合运用解析几何知识解决问题的能力.
(II)设出∠ECF=2α,表示出数量积,数量积中有cosα,
 ,确定|PC|的范围,可求出数量积的最值.
,确定|PC|的范围,可求出数量积的最值.解答:解:(I)解法一:设A,B两点坐标分别为
 ,
, ,
,由题设知

解得y12=y22=12,
所以
 ,
, 或
或 ,
, .
.设圆心C的坐标为(r,0),则
 ,
,所以圆C的方程为(x-4)2+y2=16.
解法二:设A,B两点坐标分别为(x1,y1),(x2,y2),由题设知x12+y12=x22+y22
又因为y12=2x1,y22=2x2,可得x12+2x1=x22+2x2.即(x1-x2)(x1+x2+2)=0
由x1>0,x2>0,可知x1=x2,故A,B两点关于x轴对称,所以圆心C在x轴上
设C点的坐标为(r,0),则A点坐标为
 ,于是有
,于是有 ,
,解得r=4,
所以圆C的方程为(x-4)2+y2=16.
(II)解:设∠ECF=2α,则
 .
.在Rt△PCE中,
 ,由圆的几何性质得|PC|≤|MC|+1=7+1=8,|PC|≥|MC|-1=7-1=6,
,由圆的几何性质得|PC|≤|MC|+1=7+1=8,|PC|≥|MC|-1=7-1=6,所以
 ,由此可得
,由此可得 .
.则
 的最大值为
的最大值为 ,最小值为-8.
,最小值为-8.点评:本小题主要考查平面向量,圆与抛物线的方程及几何性质等基本知识,考查综合运用解析几何知识解决问题的能力.

练习册系列答案
相关题目
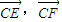 的最大值和最小值.
的最大值和最小值.