题目内容
(12分)如图 ,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,SA=AD,M为AB中点,N为SC中点.
,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,SA=AD,M为AB中点,N为SC中点.
(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SC D;
D;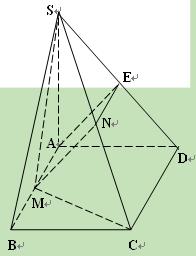
 ,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,SA=AD,M为AB中点,N为SC中点.
,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,SA=AD,M为AB中点,N为SC中点.(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SC
 D;
D;
(I)证明:取SD中点E,连接AE,NE,
∵ N、E分别是SC、SD的中点
∴ NE//CD且NE= CD
CD
∵ AB//CD且AB=CD AM= AB
AB
∴ NE//AM且NE=AM
∴ 四边形AMNE为平行四边形
∴ MN//AE
∵
∴ MN//平面S AD;
AD;
(2)∵SA⊥平面ABCD
∴ SA⊥CD
 底面ABCD为矩形,
底面ABCD为矩形,
∴ AD⊥CD
又∵SA∩AD=A ∴CD⊥平面SAD, ∴CD⊥SD ∴CD⊥AE
∴CD⊥平面SAD, ∴CD⊥SD ∴CD⊥AE
∵SA="AD " E为SD的中点 ∴ AE⊥SD ∵ SD∩CD=D
∴ AE⊥平面SCD ∵AE//MN ∴MN⊥平面SCD ∵MN 平面MSC
平面MSC
∴平面SMC⊥平面SCD
∵ N、E分别是SC、SD的中点
∴ NE//CD且NE=
 CD
CD∵ AB//CD且AB=CD AM=
 AB
AB∴ NE//AM且NE=AM
∴ 四边形AMNE为平行四边形
∴ MN//AE
∵

∴ MN//平面S
 AD;
AD;(2)∵SA⊥平面ABCD
∴ SA⊥CD
 底面ABCD为矩形,
底面ABCD为矩形,∴ AD⊥CD
又∵SA∩AD=A
 ∴CD⊥平面SAD, ∴CD⊥SD ∴CD⊥AE
∴CD⊥平面SAD, ∴CD⊥SD ∴CD⊥AE∵SA="AD " E为SD的中点 ∴ AE⊥SD ∵ SD∩CD=D
∴ AE⊥平面SCD ∵AE//MN ∴MN⊥平面SCD ∵MN
 平面MSC
平面MSC∴平面SMC⊥平面SCD
略

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
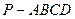 中,
中,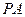 ⊥平面
⊥平面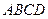 ,
,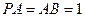 ,
,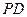 与底面
与底面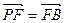 ,
, 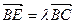
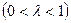 .
.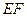 ∥平面
∥平面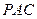 ,求
,求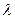 的值;
的值;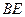 等于何值时,二面角
等于何值时,二面角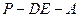 的大小为45°?
的大小为45°?
 中,高
中,高 是4米,底面的边长是6米。
是4米,底面的边长是6米。
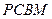 是直角梯形,∠
是直角梯形,∠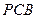 =90°,
=90°, ∥
∥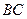 ,
,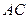 =1,∠
=1,∠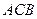 =120°,
=120°,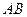 ⊥
⊥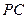 ,直线
,直线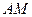 与直线
与直线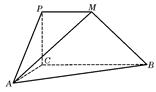
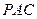 ⊥平面
⊥平面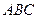 ;
;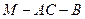 的余弦值.
的余弦值.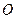 为锐角△
为锐角△ 的外心,
的外心,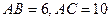
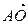 =
=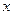
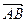 +
+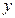
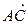 ,且
,且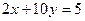 ,求
,求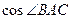 的值.
的值. ,则点
,则点 关于y轴的对称点的坐标为( )
关于y轴的对称点的坐标为( )



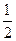 ),则l与m垂直.
),则l与m垂直. 、
、 是非零向量且满足
是非零向量且满足 ,
, ,则
,则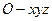 中,满足条件
中,满足条件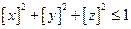 的点
的点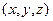 构成的空间区域
构成的空间区域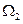 的体积为
的体积为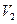 (
(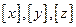 分别表示不大于
分别表示不大于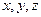 的最大整数),则
的最大整数),则