题目内容
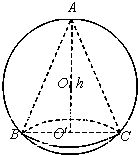
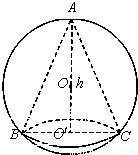
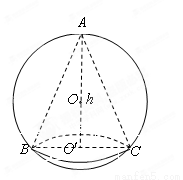
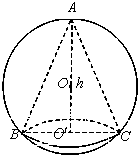
如图,已知球的半径为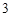 ,球内接圆锥的高为
,球内接圆锥的高为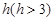 ,体积为
,体积为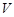 ,
,
(1)写出以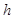 表示
表示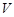 的函数关系式
的函数关系式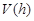 ;
;
(2)当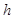 为何值时,
为何值时,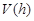 有最大值,并求出该最大值.
有最大值,并求出该最大值.
【答案】
(1)  ;
;
(2)  时,
时,
【解析】本试题主要考查了导数在研究最值问题中的运用。
利用已知条件,设出变量 ,然后得到
,然后得到
借助于函数求解导数,然后判定单调性得到最值。
解:(1)连接 ,设
,设 ,有
,有 ,
, ,则有
,则有

 ,即
,即 .
.
 分
分

 分
分
(2)  ,当
,当 ,
, ,
, 单增;
单增;
当 ,
, ,
, 单减;
单减; .
.
 分
分
当 时,
时, .
.
 分
分

练习册系列答案
相关题目
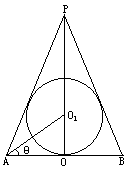
 如图,已知球的半径为定值R,球内接圆锥的高为h(h>R),体积为V,
如图,已知球的半径为定值R,球内接圆锥的高为h(h>R),体积为V,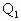 的半径为R,内切于顶点为P的圆锥(轴截面如图).设∠
的半径为R,内切于顶点为P的圆锥(轴截面如图).设∠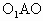 =θ.
=θ.