题目内容
将函数f(x)=sin2x-
cos2x的图象向右移动φ(φ>0)个单位,所得图象刚好关于原点对称,则φ的最小值为( )
| 3 |
分析:先利用辅助角公式化简函数,再利用图象的变换方法,结合所得图象刚好关于原点对称,可得函数为奇函数,从而可求φ的最小值.
解答:解:由于函数f(x)=sin2x-
cos2x=2sin(2x-
),向右移动φ(φ>0)个单位后得到t=2sin[2(x-φ)-
]=2sin(2x-2φ-
)的图象.
再由t=2sin(2x-2φ-
)的图象关于原点对称,可得函数t为奇函数.
∴sin(-2φ-
)=0,
∴-2φ-
=kπ,
∴φ=-
-
(k∈Z),
∴k=-1时,φ的最小正值为
.
故选D.
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
再由t=2sin(2x-2φ-
| π |
| 3 |
∴sin(-2φ-
| π |
| 3 |
∴-2φ-
| π |
| 3 |
∴φ=-
| kπ |
| 2 |
| π |
| 6 |
∴k=-1时,φ的最小正值为
| π |
| 3 |
故选D.
点评:本题主要考查两角和差的正弦公式,正弦函数的奇偶性,函数y=Asin(ωx+φ)的图象变换,属于中档题.

练习册系列答案
相关题目
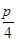 个单位,则所得到的图象对应的函数的一个单调递增区间是
个单位,则所得到的图象对应的函数的一个单调递增区间是 ) C.(
) C.(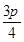 ) D.(
) D.(