题目内容
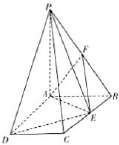 如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.(1)证明:PE⊥AF;
(2)当CE=
| 2 |
分析:(1)由题意可得此题是证明线面垂直的问题,即证明直线AF垂直于平面PBE,而当点E在BC上无论怎样运动时直线PE都在此平面内,因此只需证明已知直线垂直于平面内的两条相交直线即可.
(2)过A作AG⊥DG于G,连PG,根据二面角的定义可得∠PAG是二面角P-DE-A的平面角,由PD与平面ABCD所成角是30°,CE=
,PA=AB=1,解Rt△PAG可得二面角P-DE-A的大小.
(2)过A作AG⊥DG于G,连PG,根据二面角的定义可得∠PAG是二面角P-DE-A的平面角,由PD与平面ABCD所成角是30°,CE=
| 2 |
解答: 证明:(1)∵PA⊥平面ABCD,BE?平面ABCD,
证明:(1)∵PA⊥平面ABCD,BE?平面ABCD,
∴EB⊥PA,
又∵EB⊥AB,AB∩AP=A,AB,AP?平面PAB,
∴EB⊥平面PAB,
又∵AF?平面PAB,
∴AF⊥BE,
又∵PA=AB=1,点F是PB的中点,
∴AF⊥平面PBE.
∵PE?平面PBE,
∴AF⊥PE.
(2)过A作AG⊥DG于G,连PG,
∵DE⊥PA,
∴DE⊥平面PAG,则∠PAG是二面角P-DE-A的平面角,
∵PD与平面ABCD所成角是30°,
∴∠PDA=30°,
又∵PA=AB=1.ABCD为矩形
∴AD=
又∵CE=
,
∴DE=
S△ADE=
DE•AG=
×
×1=
=
×
AG
∴AG=1,PG=
在Rt△PAG中,cos∠PAG=
=
=
∴二面角P-DE-A的大小为45°
 证明:(1)∵PA⊥平面ABCD,BE?平面ABCD,
证明:(1)∵PA⊥平面ABCD,BE?平面ABCD,∴EB⊥PA,
又∵EB⊥AB,AB∩AP=A,AB,AP?平面PAB,
∴EB⊥平面PAB,
又∵AF?平面PAB,
∴AF⊥BE,
又∵PA=AB=1,点F是PB的中点,
∴AF⊥平面PBE.
∵PE?平面PBE,
∴AF⊥PE.
(2)过A作AG⊥DG于G,连PG,
∵DE⊥PA,
∴DE⊥平面PAG,则∠PAG是二面角P-DE-A的平面角,
∵PD与平面ABCD所成角是30°,
∴∠PDA=30°,
又∵PA=AB=1.ABCD为矩形
∴AD=
| 3 |
又∵CE=
| 2 |
∴DE=
| 3 |
S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴AG=1,PG=
| 2 |
在Rt△PAG中,cos∠PAG=
| AG |
| PG |
| 1 | ||
|
| ||
| 2 |
∴二面角P-DE-A的大小为45°
点评:解决此类问题的关键是熟悉几何体的结构特征,得到有关线面垂直、线线垂直的结论,以及利用这些垂直关系解决二面角问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点. 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2, (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.