题目内容
已知集合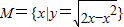 ,集合N={y|y=3x,x>0},则如图所示的韦恩图中阴影部分所表示的集合为( )
,集合N={y|y=3x,x>0},则如图所示的韦恩图中阴影部分所表示的集合为( )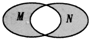
A.(2,+∞)
B.[0,1)∪(2,+∞)
C.[0,1]∪(2,+∞)
D.[0,1]∪[2,+∞)
【答案】分析:题中韦恩图的含义是在集合M∪N中不在M∩N中,由此解出M∪N和M∩N,再求出集合{x|x∈M∪N且x∉M∩N},即得本题的答案.
解答:解: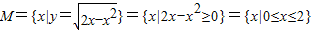 ,N={y|y=3x,x>0}={y|y>1},
,N={y|y=3x,x>0}={y|y>1},
则阴影部分为{x|x∈M∪N且x∉M∩N},M∪N={x|x≥0},M∩N={x|1<x≤2},
所以,即阴影部分为{x|x∈M∪N且x∉M∩N}={x|0≤x≤1或x>2},
即[0,1]∪(2,+∞),
故选C.
点评:本题着重考查了韦恩图的认识和集合、函数的定义域和值等基本运算等知识,属于基础题.
解答:解:
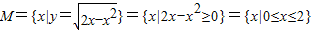 ,N={y|y=3x,x>0}={y|y>1},
,N={y|y=3x,x>0}={y|y>1},则阴影部分为{x|x∈M∪N且x∉M∩N},M∪N={x|x≥0},M∩N={x|1<x≤2},
所以,即阴影部分为{x|x∈M∪N且x∉M∩N}={x|0≤x≤1或x>2},
即[0,1]∪(2,+∞),
故选C.
点评:本题着重考查了韦恩图的认识和集合、函数的定义域和值等基本运算等知识,属于基础题.

练习册系列答案
相关题目
 ,集合N={
,集合N={ },则M
},则M N为
N为 },集合N={
},集合N={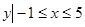 },则M
},则M (
).
(
). }
(B){
}
(B){ }
} }
(D)
}
(D)