题目内容
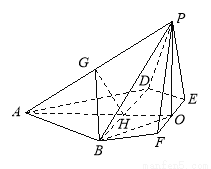
(本小题满分14分)如图,在边长为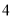 的菱形
的菱形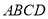 中,
中,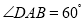 ,点
,点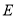 ,
,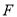 分别是边
分别是边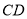 ,
, 的中点,
的中点,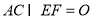 ,沿
,沿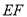 将△
将△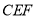 翻折到△
翻折到△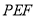 ,连接
,连接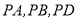 ,得到如图的五棱锥
,得到如图的五棱锥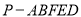 ,且
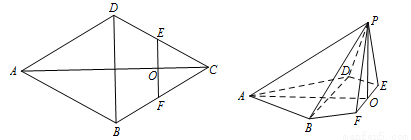
,且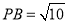 .
.
(1)求证: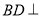 平面
平面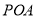 ;
;
(2)求二面角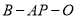 的正切值.
的正切值.
(1)证明见解析;(2)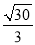 .
.
【解析】
试题分析:(1)由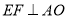 ,
,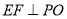 ,可证
,可证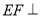 平面
平面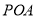 ,进而可证
,进而可证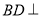 平面
平面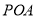 ;(2)先建立空间直角坐标系,再计算平面
;(2)先建立空间直角坐标系,再计算平面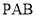 和平面
和平面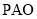 的法向量,进而可算出二面角
的法向量,进而可算出二面角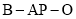 的平面角的余弦值,利用同角三角函数的基本关系,即可得二面角
的平面角的余弦值,利用同角三角函数的基本关系,即可得二面角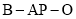 的平面角的正弦值.
的平面角的正弦值.
试题解析:(1)证明:∵点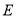 ,
,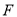 分别是边
分别是边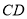 ,
,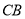 的中点,
的中点,
∴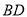 ∥
∥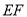 . 1分
. 1分
∵菱形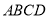 的对角线互相垂直,
的对角线互相垂直,
∴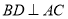 .
.
∴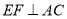 .
.
∴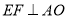 ,
,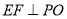 . 2分
. 2分
∵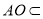 平面
平面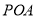 ,
,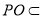 平面
平面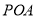 ,
,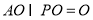 ,
,
∴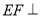 平面
平面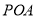 . 3分
. 3分
∴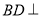 平面
平面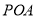 . 4分
. 4分
(2)解法1:设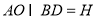 ,连接
,连接 ,
,
∵ ,
,
∴△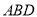 为等边三角形.
为等边三角形.
∴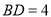 ,
,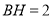 ,
,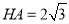 ,
,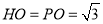 . 5分
. 5分
在R t△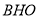 中,
中,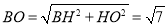 ,
,
在△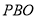 中,
中,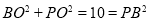 ,
,
∴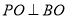 . 6分
. 6分
∵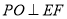 ,
,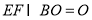 ,
,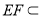 平面
平面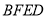 ,
,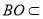 平面
平面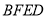 ,
,
∴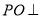 平面
平面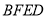 . 7分
. 7分
过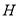 作
作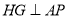 ,垂足为
,垂足为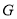 ,连接
,连接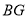 ,
,
由(1)知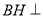 平面
平面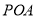 ,且
,且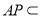 平面
平面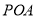 ,
,
∴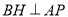 .
.
∵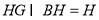 ,
,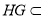 平面
平面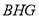 ,
,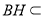 平面
平面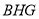 ,
,
∴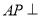 平面
平面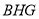 . 8分
. 8分
∵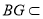 平面
平面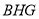 ,
,
∴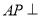
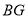 . 9分
. 9分
∴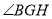 为二面角
为二面角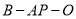 的平面角. 10分
的平面角. 10分
在Rt△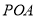 中,
中,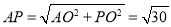 ,
,
在Rt△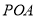 和Rt△
和Rt△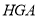 中,
中,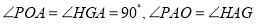 ,
,
∴Rt△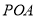 ~Rt△
~Rt△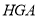 . 11分
. 11分
∴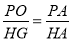 .
.
∴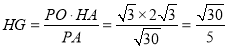 . 12分
. 12分
在Rt△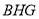 中,
中,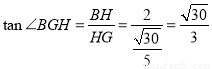 . 13分
. 13分
∴二面角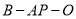 的正切值为
的正切值为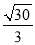 . 14分
. 14分
解法2:设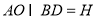 ,连接
,连接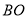 ,
,
∵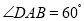 ,
,
∴△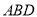 为等边三角形.
为等边三角形.
∴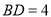 ,
,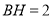 ,
,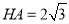 ,
,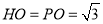 . 5分
. 5分
在R t△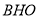 中,
中,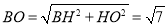 ,
,
在△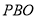 中,
中,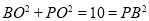 ,
,
∴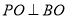 . 6分
. 6分
∵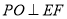 ,
,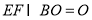 ,
,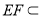 平面
平面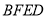 ,
,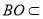 平面
平面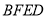 ,
,
∴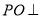 平面
平面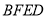 . 7分
. 7分

以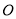 为原点,
为原点,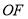 所在直线为
所在直线为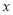 轴,
轴,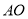 所在直线为
所在直线为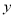 轴,
轴,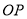 所在直线为
所在直线为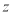 轴,建立空间直角坐标系
轴,建立空间直角坐标系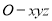 ,则
,则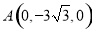 ,
,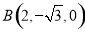 ,
,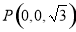 ,
,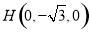 . 8分
. 8分
∴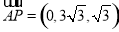 ,
,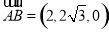 .
.
设平面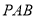 的法向量为
的法向量为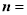
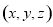 ,
,
由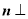
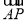 ,
,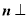
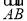 ,得
,得  9分
9分
令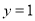 ,得
,得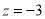 ,
,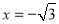 .
.
∴平面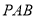 的一个法向量为
的一个法向量为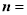
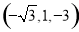 . 10分
. 10分
由(1)知平面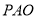 的一个法向量为
的一个法向量为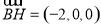 , 11分
, 11分
设二面角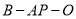 的平面角为
的平面角为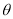 ,
,
则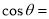
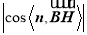

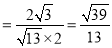 . 12分
. 12分
∴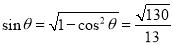 ,
,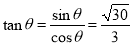 . 13分
. 13分
∴二面角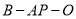 的正切值为
的正切值为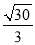 . 14分
. 14分
考点:1、线面垂直;2、二面角;3、空间向量及坐标运算;4、同角三角函数的基本关系.
考点分析: 考点1:点、线、面之间的位置关系 考点2:异面直线所成的角 考点3:线面所成的角 试题属性- 题型:
- 难度:
- 考核:
- 年级:

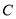 在圆
在圆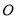 直径
直径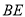 的延长线上,
的延长线上,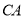 切圆
切圆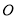 于
于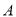 点,
点,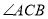 的平分线
的平分线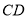 交
交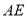 于点
于点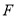 ,交
,交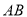 于
于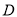 点.
点.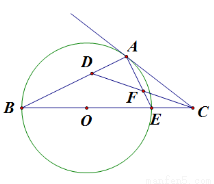
 的度数;
的度数;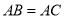 ,求
,求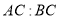 .
. 的零点个数为( )
的零点个数为( ) B.
B. C.
C. D.
D.
 满足对任意
满足对任意 ,都有
,都有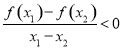 成立,则实数
成立,则实数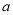 的取值范围是( )
的取值范围是( )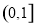 B.
B.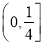 C.
C. D.
D.
 ,第二次得到的点数为
,第二次得到的点数为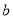 ,则事件“
,则事件“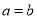 ”的概率为( )
”的概率为( )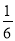 B.
B.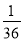 C.
C.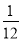 D.
D.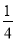
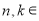 N
N ,且
,且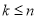 ,
,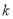 C
C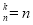 C
C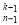 ,则可推出
,则可推出 C
C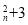 C
C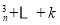 C
C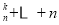 C
C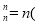 C
C C
C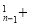
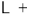 C
C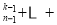 C
C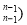
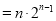 ,
,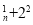 C
C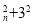 C
C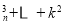 C
C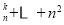 C
C .
. ,则该锥体的俯视图可以是( )
,则该锥体的俯视图可以是( )

 ,求
,求 的值
的值