题目内容

在等比数列{an}中，Sn=48,S2n=60,求S3n.

解法一：∵S2n≠2Sn,∴q≠1.

根据已知条件得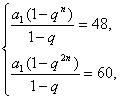两式相除得1+qn=.

∴qn=.

代入得=64.

∴S3n=(1-q3n)=64×(1-)=63.

解法二：∵{an}为等比数列，

∴(S2n-Sn)2=Sn(S3n-S2n).

∴S3n=+S2n=+60=63.

练习册系列答案
相关题目
在等比数列{an}中，a4=
2
3
 ， a3+a5=
20
9
．
（1）求数列{an}的通项公式；
（2）若数列{an}的公比大于1，且bn=log3
an
2
，求数列{bn}的前n项和Sn．
在等比数列{an}中，若a1=1，公比q=2，则a12+a22+…+an2=（　　）
A、（2n-1）2
B、
1
3
（2n-1）
C、4n-1
D、
1
3
（4n-1）
在等比数列{an}中，如果a1+a3=4，a2+a4=8，那么该数列的前8项和为（　　）
在等比数列{an}中，a1=1，8a2+a5=0，数列{
1
an
}的前n项和为Sn，则S5=（　　）
在等比数列{an}中，an＞0且a2=1-a1，a4=9-a3，则a5+a6=
81
81
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网