Question

在平面直角坐标系中，点P到两点（0，-

3

），（0，

3

）的距离之和等于4，设点P的轨迹为C．
（I）求曲线C的方程；
（Ⅱ）过点（0，

3

）作两条互相垂直的直线l₁，l₂分别与曲线C交于A，B和C，D．求四边形ACBD面积的取值范围．

Answer 1

分析：（I）根据点P到两点（0，-

3

），（0，

3

）的距离之和等于4，利用椭圆的定义，可得椭圆方程可得．
（II）分类讨论，设出直线方程和椭圆方程联立消去y，根据韦达定理求得|AB|的表达式，进而把k换为-

1

k

，求得|CD|表达式进而得到四边形ABCD的面积，令k²+1=t，根据t的范围可确定四边形ABCD的面积的范围，最后看当直线l₁或l₂的斜率有一个不存在时，另一个斜率为0，此时四边形ABCD的面积为2，综合可得答案．

解答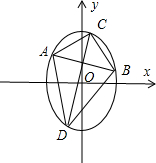：解：（I）设P（x，y），由椭圆定义可知，点P的轨迹C是以（0，-

3

），（0，

3

）为焦点，长半轴为2的椭圆．它的短半轴b=

a2-c2

=1，故曲线C的方程为x²+

y2

4

=1；
（II）①当两直线的斜率存在时，设直线l1：y=kx+

3

，A（x₁，y₁），B（x₂，y₂），
直线方程代入椭圆方程，可得（k²+4）x²+2

3

kx-1=0，
故x₁+x₂=

2 3 k

k2+4

，x₁x₂=-

1

k2+4

∴|AB|=

1+k2

|x₁-x₂|=

4(k2+1)

k2+4

将上式中的k换为-

1

k

得|CD|=

4(k2+1)

4k2+1

由于AB⊥CD，故四边形ACBD的面积为S=

1

2

|AB||CD|=

8(k2+1)2

(k2+4)(4k2+1)

令k²+1=t，则S=

8t2

(t+3)(4t-3)

=

8t2

4t2+9t-9

=

8

-9( 1 t - 1 2 )2+ 25 4

∵

1

t

∈（0，1），∴4＜-9（

1

t

-

1

2

）²+

25

4

≤

25

4

∴

32

25

≤S＜2，
②直线l₁或l₂的斜率有一个不存在时，另一个斜率为0，不难验证此时四边形ABCD的面积为2，
故四边形ACBD面积的取值范围是[

32

25

，2)．

点评：本题主要考查了椭圆的应用，考查直线与椭圆的位置关系，考查了学生对问题的综合分析和基本的运算能力，属于中档题．