题目内容
已知复数Z在复平面上对应的点位于第二象限,且(1-i)Z=1+ai(其中i是虚数单位),则实数a的取值范围是
- A.(1,+∞)
- B.(-1,1)
- C.(-∞,-1)
- D.(-∞,-1)∪(1,+∞)
A
分析:由(1-i)Z=1+ai,解得 Z= ,再利用两个复数代数形式的除法法则求得结果为
,再利用两个复数代数形式的除法法则求得结果为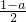 +
+ ,再由Z在复平面上对应的点位于第二象限,可得
,再由Z在复平面上对应的点位于第二象限,可得 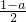 <0,且
<0,且  >0,解不等式求得实数a的取值范围.
>0,解不等式求得实数a的取值范围.
解答:∵(1-i)Z=1+ai,∴Z= =
= =
= =
=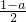 +
+ ,
,
复数Z在复平面上对应的点位于第二象限,
∴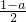 <0,且
<0,且  >0.
>0.
解得 a>1,
故选 A.
点评:本题主要考查复数代数表示法及其几何意义,两个复数代数形式的除法,属于基础题.
分析:由(1-i)Z=1+ai,解得 Z=
 ,再利用两个复数代数形式的除法法则求得结果为
,再利用两个复数代数形式的除法法则求得结果为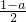 +
+ ,再由Z在复平面上对应的点位于第二象限,可得
,再由Z在复平面上对应的点位于第二象限,可得 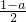 <0,且
<0,且  >0,解不等式求得实数a的取值范围.
>0,解不等式求得实数a的取值范围.解答:∵(1-i)Z=1+ai,∴Z=
 =
= =
= =
=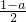 +
+ ,
,复数Z在复平面上对应的点位于第二象限,
∴
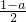 <0,且
<0,且  >0.
>0.解得 a>1,
故选 A.
点评:本题主要考查复数代数表示法及其几何意义,两个复数代数形式的除法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目