题目内容
已知f(x)=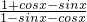 +
+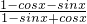 .
.
(I)化简f(x);
(II) 是否存在x,使得tan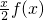 与
与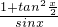 相等?若存在,求x的值,若不存在,请说明理由.
相等?若存在,求x的值,若不存在,请说明理由.
解:(I)f(x)=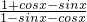 +
+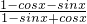
=
=
=
=-2cscx且x≠2kπ+ (k∈Z)
(k∈Z)
(II) =
= ,
,
1+(tan )2=
)2= ,
,
tan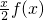 =
= =
= ,
,
sinx=-1,x=2kπ- (k为任意整数)
(k为任意整数)
存在,此时x=2kπ+ ,k∈Z.
,k∈Z.
分析:(I)对f(x)=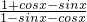 +
+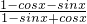 .同分,分子、分母按多项式乘法展开,利用基本关系式直接化简f(x);
.同分,分子、分母按多项式乘法展开,利用基本关系式直接化简f(x);
(II) 存在x,化简tan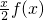 与
与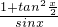 ,然后令二者相等,求解x的值即可.
,然后令二者相等,求解x的值即可.
点评:本题考查同角三角函数基本关系的运用,弦切互化,考查计算能力,是中档题.
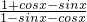 +
+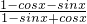
=

=

=

=-2cscx且x≠2kπ+
 (k∈Z)
(k∈Z)(II)
 =
= ,
,1+(tan
 )2=
)2= ,
,tan
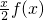 =
= =
= ,
,sinx=-1,x=2kπ-
 (k为任意整数)
(k为任意整数)存在,此时x=2kπ+
 ,k∈Z.
,k∈Z.分析:(I)对f(x)=
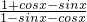 +
+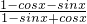 .同分,分子、分母按多项式乘法展开,利用基本关系式直接化简f(x);
.同分,分子、分母按多项式乘法展开,利用基本关系式直接化简f(x);(II) 存在x,化简tan
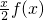 与
与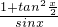 ,然后令二者相等,求解x的值即可.
,然后令二者相等,求解x的值即可.点评:本题考查同角三角函数基本关系的运用,弦切互化,考查计算能力,是中档题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目