题目内容
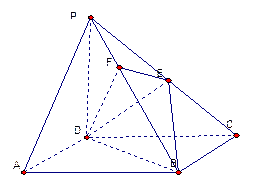
(本小题满分14分)如图,在四棱锥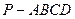 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱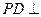 底面ABCD,
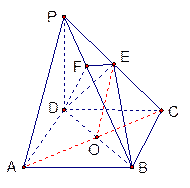
底面ABCD,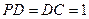 ,E是PC的中点,作
,E是PC的中点,作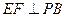 交PB于点F.
交PB于点F.
(I) 证明:PA∥平面EDB;
(II) 证明:PB⊥平面EFD;
(III) 求三棱锥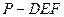 的体积.
的体积.
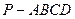 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱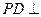 底面ABCD,
底面ABCD,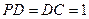 ,E是PC的中点,作
,E是PC的中点,作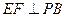 交PB于点F.
交PB于点F.(I) 证明:PA∥平面EDB;
(II) 证明:PB⊥平面EFD;
(III) 求三棱锥
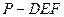 的体积.
的体积.
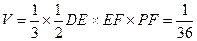
解:(1)证明:连结AC,AC交BD于O,连结EO
∵底面ABCD是正方形,∴点O是AC的中点
在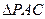 中,EO是中位线,∴PA // EO
中,EO是中位线,∴PA // EO
而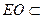 平面EDB且
平面EDB且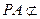 平面EDB,
平面EDB,
所以,PA // 平面EDB. ................4分
(2)证明:∵PD⊥底面ABCD且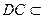 底面ABCD,∴
底面ABCD,∴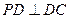
∵PD=DC,可知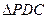 是等腰直角三角形,而DE是斜边PC的中线,
是等腰直角三角形,而DE是斜边PC的中线,
 ∴
∴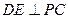 ①
①
同样由PD⊥底面ABCD,得PD⊥BC
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC
而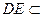 平面PDC,∴
平面PDC,∴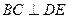 ②
②
由①和②推得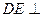 平面PBC
平面PBC
而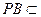 平面PBC,∴
平面PBC,∴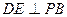
又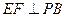 且
且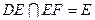 ,所以PB⊥平面EFD
,所以PB⊥平面EFD
.................8分
(3)∵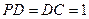 ,
,
由PD⊥平面ABCD,∴PD⊥BC,
又∵BC⊥CD,PD∩CD=D,∴BC⊥平面PCD,
∴BC⊥PC.
在△BDE中,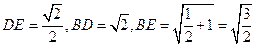 ,
,
∴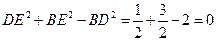 ,即DE⊥BE.
,即DE⊥BE.
而由(2),PB⊥平面EFD,有PB⊥DE,因而DE⊥平面BEF,
在Rt△BPD中,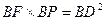 ,
,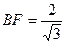 ;Rt△BEF中,
;Rt△BEF中,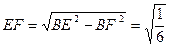 .
.
∴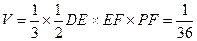 . ........14分
. ........14分
∵底面ABCD是正方形,∴点O是AC的中点
在
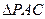 中,EO是中位线,∴PA // EO
中,EO是中位线,∴PA // EO而
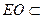 平面EDB且
平面EDB且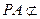 平面EDB,
平面EDB,所以,PA // 平面EDB. ................4分
(2)证明:∵PD⊥底面ABCD且
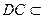 底面ABCD,∴
底面ABCD,∴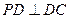
∵PD=DC,可知
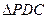 是等腰直角三角形,而DE是斜边PC的中线,
是等腰直角三角形,而DE是斜边PC的中线, ∴
∴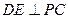 ①
①同样由PD⊥底面ABCD,得PD⊥BC
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC
而
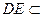 平面PDC,∴
平面PDC,∴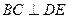 ②
②由①和②推得
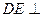 平面PBC
平面PBC而
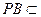 平面PBC,∴
平面PBC,∴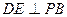
又
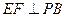 且
且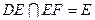 ,所以PB⊥平面EFD
,所以PB⊥平面EFD.................8分
(3)∵
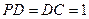 ,
,由PD⊥平面ABCD,∴PD⊥BC,
又∵BC⊥CD,PD∩CD=D,∴BC⊥平面PCD,
∴BC⊥PC.
在△BDE中,
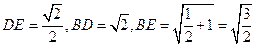 ,
,∴
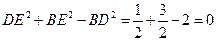 ,即DE⊥BE.
,即DE⊥BE.而由(2),PB⊥平面EFD,有PB⊥DE,因而DE⊥平面BEF,
在Rt△BPD中,
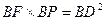 ,
,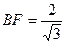 ;Rt△BEF中,
;Rt△BEF中,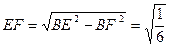 .
.∴
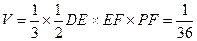 . ........14分
. ........14分
练习册系列答案
相关题目
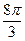
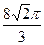
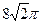
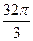
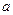 正四面体的表面积是( )
正四面体的表面积是( )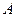 、
、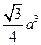 ;
; 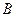 、
、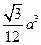 ;
; 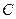 、
、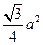 ;
; 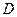 、
、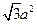 。
。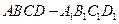 中,
中,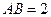 ,
,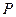 是
是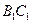 的中点,则四棱锥
的中点,则四棱锥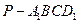 的体积为____★______.
的体积为____★______.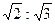
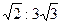
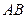 所在直线方程为
所在直线方程为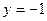 ,线段
,线段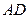 所在直线方程为
所在直线方程为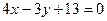 ,线段
,线段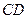 所在直线方程为
所在直线方程为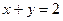 ,求四边形
,求四边形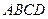 绕
绕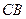 所在直线旋转一周所围成的几何体的表面积和体积
所在直线旋转一周所围成的几何体的表面积和体积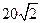
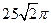
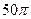
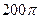 [
[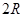 ,则该圆锥的体积为 ( )
,则该圆锥的体积为 ( )