题目内容
如图,已知抛物线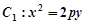 的焦点在抛物线
的焦点在抛物线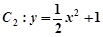 上,点
上,点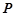 是抛物线
是抛物线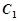 上的动点.
上的动点.
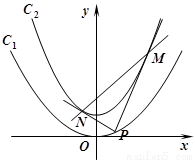
(Ⅰ)求抛物线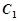 的方程及其准线方程;
的方程及其准线方程;
(Ⅱ)过点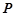 作抛物线
作抛物线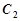 的两条切线,
的两条切线,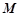 、
、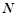 分别为两个切点,设点
分别为两个切点,设点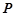 到直线
到直线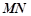 的距离为
的距离为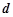 ,求
,求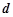 的最小值.
的最小值.
【答案】
(1)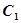 的方程为
的方程为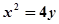 ,其准线方程为
,其准线方程为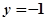 .(2)
.(2)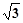
【解析】
试题分析:解:(Ⅰ)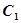 的焦点为
的焦点为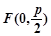 , …2分
, …2分
所以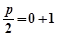 ,
,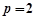 . …4分
. …4分
故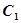 的方程为
的方程为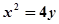 ,其准线方程为
,其准线方程为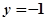 . …6分
. …6分
(Ⅱ)设 ,
,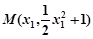 ,
,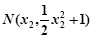 ,
,
则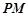 的方程:
的方程: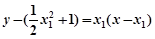 ,
,
所以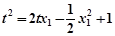 ,即
,即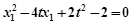 .
.
同理,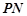 :
: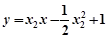 ,
,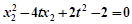 . …8分
. …8分
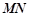 的方程:
的方程: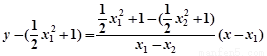 ,
,
即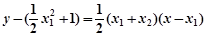 .
.
由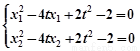 ,得
,得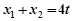 ,
,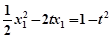 . …10分
. …10分
所以直线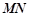 的方程为
的方程为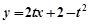 . …12分
. …12分
于是 .
.
令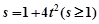 ,则
,则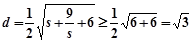 (当
(当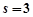 时取等号).
时取等号).
所以,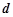 的最小值为
的最小值为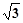 . …15分
. …15分
考点:抛物线方程
点评:解决的关键是对于直线与抛物线的位置关系的运用,联立方程组,结合韦达定理来求解,属于基础题。

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 的焦点在抛物线
的焦点在抛物线 上.
上.
 的方程及其准线方程;
的方程及其准线方程; 作抛物线
作抛物线 的两条切线
的两条切线 、
、 , 切点为
, 切点为 、
、 .若
.若 ,且
,且 ,求
,求 的取值范围.
的取值范围.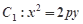 的焦点在抛物线
的焦点在抛物线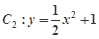 上.
上.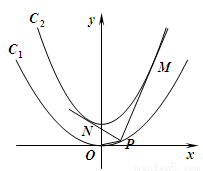
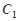 的方程及其准线方程;
的方程及其准线方程;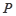 作抛物线
作抛物线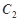 的两条切线
的两条切线 、
、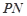 , 切点为
, 切点为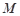 、
、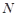 .若
.若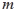 ,且
,且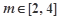 ,求
,求 的取值范围.
的取值范围. 的焦点F恰好是双曲线
的焦点F恰好是双曲线 的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
 B.
B. C.
C. D.
D. 
 如图,已知抛物线
如图,已知抛物线 的焦点在抛物线
的焦点在抛物线 上,点P是抛物线C1上的动点.
上,点P是抛物线C1上的动点.