Question

设等比数列{a_n}的公比为q，前n项和为S_n，且a₁＞0．若S₂＞2a₃，则q的取值范围是

1. A.
   
2. B.
   
3. C.
   
4. D.
   

Answer 1

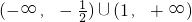
B
分析：由题意可得a₁＞0，且 a₁+a₁q＞2a₁q²，解一元二次不等式求得q的取值范围，注意 q≠0这个隐藏条件．
解答：由题意可得a₁＞0，且 a₁+a₁q＞2a₁q²，即 2q²-q-1＜0，即 （2q+1）（q-1）＜0．
解得-＜q＜1，又 q≠0，∴q的取值范围是 ，
故选B．
点评：本题主要考查数列的函数特性，等比数列的通项公式，一元二次不等式的解法，注意 q≠0这个隐藏条件，
这是解题的易错点，属于中档题．