题目内容
设函数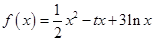 ,
,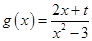 ,已知
,已知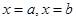 为函数
为函数 的极值点
的极值点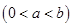
(1)求函数 在
在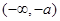 上的单调区间,并说明理由.
上的单调区间,并说明理由.
(2)若曲线 在
在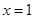 处的切线斜率为-4,且方程
处的切线斜率为-4,且方程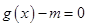 有两个不相等的负实根,求实数
有两个不相等的负实根,求实数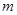 的取值范围.
的取值范围.
(1)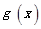 的单调增区间为
的单调增区间为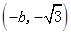 和
和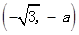 ,
,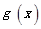 的单调减区间为
的单调减区间为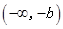
(2)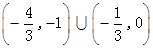 .
.
解析试题分析:(1)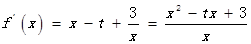 ,
,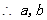 为方程
为方程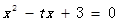 的两根
的两根
又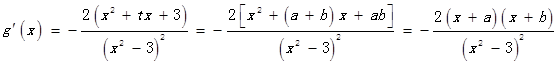
由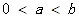 及
及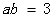 知:
知:
当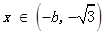 和
和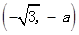 时,
时,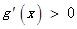 ,当
,当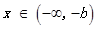 时,
时,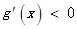
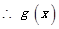 的单调增区间为
的单调增区间为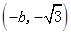 和
和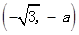 ,
,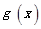 的单调减区间为
的单调减区间为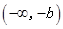
(2)由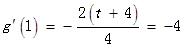 得
得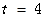
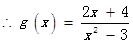
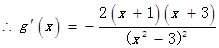
令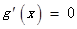 得
得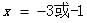
当 在
在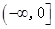 上变化时,
上变化时,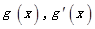 的变化情况如下:
的变化情况如下: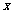
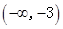
-3 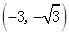
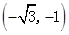
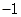 -
-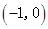
0 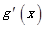
- 0 + + 0 - 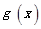
↘ 极小值 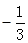
↗ 练习册系列答案
练习册系列答案
课时掌控系列答案
乐享导学练习系列答案
快乐5加2课课优优系列答案
全科王同步课时练习系列答案
高效通教材精析精练系列答案
课堂导练1加5系列答案
探究在线高效课堂系列答案
千里马测试卷全新升级版系列答案
助教型教辅领航课堂系列答案
尖子生单元突破系列答案
相关题目
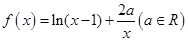
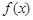 的单调区间;
的单调区间;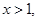 且
且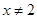 时,
时,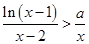 恒成立,求实数
恒成立,求实数 的范围.
的范围.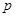 与死亡年数
与死亡年数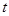 之间的函数关系式;
之间的函数关系式; )
) 是定义域为
是定义域为 的奇函数,(1)求实数
的奇函数,(1)求实数 的值;(2)证明
的值;(2)证明 是
是 ,不等式
,不等式 恒成立,求
恒成立,求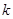 的取值范围.
的取值范围.
 的不等式
的不等式 ;
; 的图象恒在函数
的图象恒在函数 图象的上方(没有公共点),求
图象的上方(没有公共点),求 的取值范围。
的取值范围。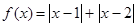 .
.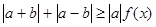 ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.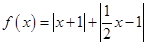 .
.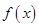 的图象,写出函数
的图象,写出函数 的不等式
的不等式
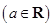 .
.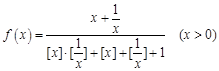 ,其中
,其中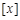 表示不超过
表示不超过 的最大整数,如
的最大整数,如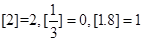 .
.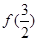 的值;
的值;  上存在x,使得
上存在x,使得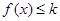 成立,求实数k的取值范围;
成立,求实数k的取值范围; 的值域.
的值域.