题目内容
已知随机变量ξ的分布列如表所示:| x | -1 | 1 | 2 | |
| P(ξ=x) | a | b | c |  |
【答案】分析:由分布列的性质和期望方差的定义可得a+b+c+ =1,①-a+c+
=1,①-a+c+ =0,②a+c+
=0,②a+c+ =1,③联立解方程组可得.
=1,③联立解方程组可得.
解答:解:由分布列的性质可得a+b+c+ =1,①
=1,①
又可得Eξ=-a+c+ =-a+c+
=-a+c+ =0,②
=0,②
Dξ=(-1-0)2a+(0-0)2b+(1-0)2c+(2-0)2× =1,
=1,
化简可得:a+c+ =1,③
=1,③
联立②③可解得 ,代入①可得b=
,代入①可得b=
故答案为:
点评:本题考查离散型随机变量的期望与方程,涉及分布列的性质的应用,属中档题.
 =1,①-a+c+
=1,①-a+c+ =0,②a+c+
=0,②a+c+ =1,③联立解方程组可得.
=1,③联立解方程组可得.解答:解:由分布列的性质可得a+b+c+
 =1,①
=1,①又可得Eξ=-a+c+
 =-a+c+
=-a+c+ =0,②
=0,②Dξ=(-1-0)2a+(0-0)2b+(1-0)2c+(2-0)2×
 =1,
=1,化简可得:a+c+
 =1,③
=1,③联立②③可解得
 ,代入①可得b=
,代入①可得b=
故答案为:

点评:本题考查离散型随机变量的期望与方程,涉及分布列的性质的应用,属中档题.

练习册系列答案
相关题目
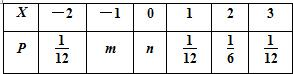 已知随机变量X的分布列如图:其中m,n∈[0,1),且E(X)=
已知随机变量X的分布列如图:其中m,n∈[0,1),且E(X)=| 1 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|