题目内容
【题目】已知函数![]() .
.
(1)过原点![]() 作函数
作函数![]() 图象的切线,求切点的横坐标;
图象的切线,求切点的横坐标;
(2)对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(1)设切点坐标,利用导数几何意义以及切点在切线上,也在曲线上列方程组,解得切点的横坐标;(2)不等式恒成立问题往往转化为对应函数最值问题: ![]() 对
对![]() ,
, ![]() 恒成立等价于
恒成立等价于![]() 的最小值不小于零,根据导函数符号变化规律,分类讨论函数单调性,进而得函数最值,验证是否满足条件,确定实数
的最小值不小于零,根据导函数符号变化规律,分类讨论函数单调性,进而得函数最值,验证是否满足条件,确定实数![]() 的取值范围.
的取值范围.
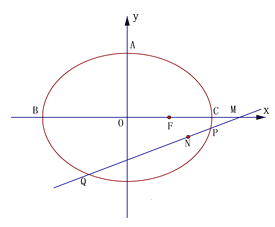
试题解析:(Ⅰ)设切点为![]() ,直线的切线方程为
,直线的切线方程为![]()
, ![]() ,
,
即直线的切线方程为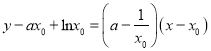
又切线过原点![]() ,所以
,所以![]() ,
,
由![]() ,解得
,解得![]() ,所以切点的横坐标为
,所以切点的横坐标为![]() .
.
(Ⅱ)方法一:∵不等式![]() 对
对![]() ,
, ![]() 恒成立,
恒成立,
∴![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
设![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() ,
, ![]() 上单调递减,
上单调递减,
即![]() ,
, ![]() 不符合题意.
不符合题意.
②当![]() 时,
时, ![]() .设
.设![]() ,
,
在![]() ,
, ![]() 上单调递增,即
上单调递增,即![]() .
.
(ⅰ)当![]() 时,由
时,由![]() ,得
,得![]() ,
, ![]() 在
在![]() ,
, ![]() 上单调递增,即
上单调递增,即![]() ,
, ![]() 符合题意;
符合题意;
(ii)当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 使得
使得![]() ,
,
则![]() 在
在![]() ,
, ![]() 上单调递减,在
上单调递减,在![]() ,
, ![]() 上单调递增,
上单调递增,
![]() ,则
,则![]() 不合题意.
不合题意.
综上所述, ![]() .
.
(Ⅱ)方法二:∵不等式![]() 对
对![]() ,
, ![]() 恒成立,
恒成立,
∴![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
![]() 不恒成立;同理
不恒成立;同理![]() 取其他值不恒成立.
取其他值不恒成立.
当![]() 时,
时, ![]() 恒成立;
恒成立;
当![]() 时,
时, ![]() ,证明
,证明![]() 恒成立.
恒成立.
设![]()
![]() ,
, ![]() ,
,
![]() .∴
.∴![]() 在
在![]() ,
, ![]() 为减函数.
为减函数.
![]() ,∴
,∴![]() .
.
(Ⅱ)方法三:∵不等式![]() 对
对![]() ,
,![]() 恒成立,
恒成立,
∴等价于![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
设![]() ,当
,当![]() 时,
时, ![]() ;∴
;∴![]() ,
,
函数![]() 过点(0,0)和(1,0),函数
过点(0,0)和(1,0),函数![]() 过点(1.0),
过点(1.0),![]() 在
在![]() 恒成立,
恒成立,
一定存在一条过点(1,0)的直线和函数![]() 、
、![]() 都相切或,一定存在一条过点(1,0)的直线
都相切或,一定存在一条过点(1,0)的直线![]() 相切和函数
相切和函数![]() 相交,但交点横坐标小于1,
相交,但交点横坐标小于1,
当都相切时![]() .
.
![]() 不大于等于0.
不大于等于0.
∴![]() .
.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目