题目内容
把下列角化成2kπ+α(0≤α<2π,k∈Z)的形式,并指出它们是第几象限角,写出与其终边相同的角的集合.
(1)-
;
(2)-20.
(1)-
| 46π | 3 |
(2)-20.
分析:利用与α终边相同的角的集合的结论,即可求得结论.
解答:解:(1)-
=-8×2π+
,它是第二象限角,与-
终边相同的角的集合为{a|a=2kπ+
,k∈Z};(2)-20=-4×2π+(8π-20),而
π<8π-20<2π,∴-20是第四象限角,与-20终边相同的角的集合为{α|α=2kπ+(8π-20),k∈Z}.
| 46π |
| 3 |
| 2π |
| 3 |
| 46π |
| 3 |
| 2π |
| 3 |
| 3 |
| 2 |
点评:本题考查终边相同的角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
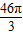 ;
;