题目内容
已知函数
 ,数列
,数列 是公差为d的等差数列,
是公差为d的等差数列, 是公比为q(
是公比为q( )的等比数列.若
)的等比数列.若



(Ⅰ)求数列
 ,
, 的通项公式;
的通项公式; (Ⅱ)设数列
 对任意自然数n均有
对任意自然数n均有 ,求
,求 的值;
的值;(Ⅲ)试比较
 与
与 的大小.
的大小.(1)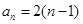 ,
, (2)
(2)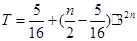 (3)
(3)
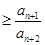
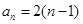 ,
, (2)
(2)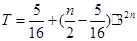 (3)
(3)
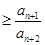
试题分析:(Ⅰ) ∵
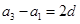 , ∴
, ∴ 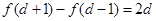 .
. 即
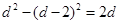 , 解得 d =2.
, 解得 d =2.∴
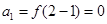 . ∴
. ∴ 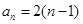 2分
2分∵
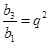 , ∴
, ∴ 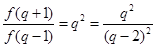 .
.∵
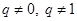 , ∴
, ∴ 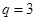 .
.又
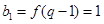 , ∴
, ∴  . 4分
. 4分(Ⅱ) 由题设知
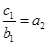 , ∴
, ∴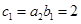 .
.当
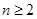 时,
时, 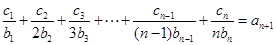 ,
,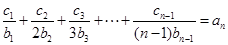 ,
,两式相减,得
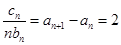 .
.∴
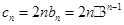 (
(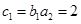 适合). 7分
适合). 7分设T=
 ,
,∴

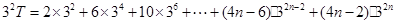
两式相减 ,得
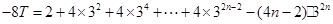
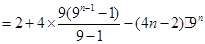
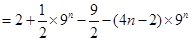
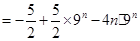 .
.∴
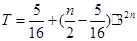 . 10分
. 10分(Ⅲ)

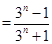
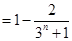 ,
, 
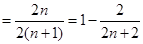 .
.现只须比较
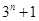 与
与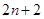 的大小.
的大小.当n=1时,
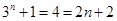 ;
;当n=2时,
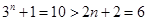 ;
;当n=3时,
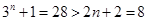 ;
;当n=4时,
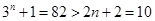 .
.猜想
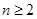 时,
时,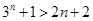 . 12分
. 12分 用数学归纳法证明
(1)当n=2时,左边
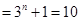 ,右边
,右边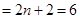 ,
,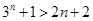 成立.
成立.(2)假设当n=k时, 不等式成立,即
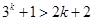 .
.当n=k+1时,
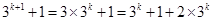
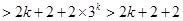
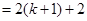 .
.即当n=k+1时,不等式也成立.
由(1)(2),可知
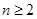 时,
时,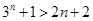 都成立.
都成立.所以
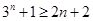 (当且仅当n=1时,等号成立)
(当且仅当n=1时,等号成立)所以
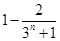
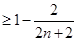 .即
.即
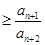 . 14分
. 14分点评:主要是考查了等差数列和等比数列的通项公式和求和运用,以及数学归纳法来猜想证明大小,属于难度试题。

练习册系列答案
相关题目
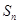 是数列
是数列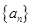 的前
的前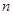 项和,且对任意
项和,且对任意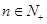 ,有
,有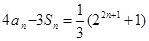 ,
,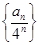 的通项公式;
的通项公式;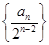 的前
的前 .
. 的一个通项公式是
的一个通项公式是



 的各项均为正数,且
的各项均为正数,且 ,则
,则








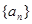 中,al =" l," a2 =" 2+3" , a3 =" 4+5+6" , a4 =" 7+8+9+10" , ……,则a10的值是_______
中,al =" l," a2 =" 2+3" , a3 =" 4+5+6" , a4 =" 7+8+9+10" , ……,则a10的值是_______ 中,当
中,当 时,总有
时,总有 成立,且
成立,且 .
. 是等差数列,并求数列
是等差数列,并求数列 项和
项和 .
. 满足
满足 .
. ,并由此猜想
,并由此猜想 的一个通项公式,证明你的结论;
的一个通项公式,证明你的结论; ,不等式
,不等式 对一切
对一切 都成立,求正整数m的最大值。
都成立,求正整数m的最大值。 满足
满足 ,
, ,则它的前10项的和
,则它的前10项的和 _____
_____ 的前
的前 项和
项和 ,且
,且 成等比数列.
成等比数列. 满足
满足 ,求
,求 项和
项和 .
.