题目内容
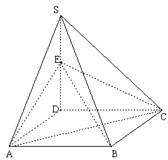 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.SD=2,
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.SD=2,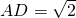 ,E是SD上的点.
,E是SD上的点.
(Ⅰ)求证:AC⊥BE;
(Ⅱ)求二面角C-AS-D的余弦值.
 解:法一(Ⅰ)连接BD.因为底面ABCD是正方形,
解:法一(Ⅰ)连接BD.因为底面ABCD是正方形,所以AC⊥BD.因为SD⊥平面ABCD,
AC?平面ABCD,所以AC⊥SD. (2分)
又因为SD∩BD=D,所以AC⊥平面BDS. (4分)
因为BE?平面BDS,所以AC⊥BE. (6分)
(Ⅱ)因为SD⊥平面ABCD,所以SD⊥CD.
因为底面ABCD是正方形,所以AD⊥CD.
又因为SD∩AD=D,所以CD⊥平面SAD,
所以CD⊥AS. (8分)
过点D在平面SAD内作DF⊥AS于F,连接CF.
由于,DF∩CD=D,所以AS⊥平面DCF.所以AS⊥CF.
故∠CFD是二面角C-AS-D的平面角. (10分)
在Rt△ADS中,SD=2,
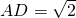 ,可求得
,可求得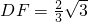 .
.在Rt△CFD中,
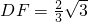 ,
, ,可求得
,可求得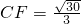 .
.所以
 .即二面角C-AS-D的余弦值为
.即二面角C-AS-D的余弦值为 .(12分)
.(12分)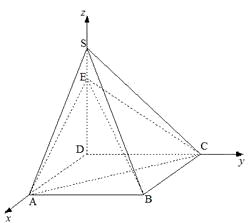 法二:(Ⅰ)如图以D为原点建立空间直角坐标系D-xyz.
法二:(Ⅰ)如图以D为原点建立空间直角坐标系D-xyz.则D(0,0,0),A(
 ,0,0),B(
,0,0),B( ,
, ,0),
,0),C(0,
 ,0),E(0,0,
,0),E(0,0, ),S(0,0,2),
),S(0,0,2), ,
, =
=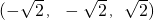 . (3分)
. (3分) •
• =2-2+0=0,所以
=2-2+0=0,所以 ⊥
⊥ .即AC⊥BE. (6分)
.即AC⊥BE. (6分)(Ⅱ)由(Ⅰ)得
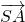 =(
=( ,0,-2),
,0,-2), =(0,
=(0, ,-2).
,-2).设平面ACS的法向量为
 =(x,y,z),
=(x,y,z),则由n⊥
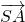 ,n⊥
,n⊥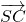 得
得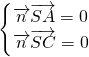 ,即
,即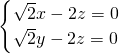
取
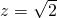 ,得
,得 . (9分)
. (9分)易知平面ASD的一个法向量为
 =(0,
=(0, ,0).
,0).设二面角C-AS-D的平面角为θ.则
 .
.即二面角C-AS-D的余弦值为
 . (12分)
. (12分)分析:法一(Ⅰ)连接BD,证明AC垂直平面BDS内的两条相交直线SD,BD,即可证明AC⊥平面BDS,从而证明AC⊥BE;
(Ⅱ)过点D在平面SAD内作DF⊥AS于F,连接CF.说明∠CFD是二面角C-AS-D的平面角,通过解三角形CFD求二面角C-AS-D的余弦值.
法二:以D为原点建立空间直角坐标系D-xyz.
(Ⅰ)求出
 ,
, ,计算
,计算 •
• =0,即可证明AC⊥BE;
=0,即可证明AC⊥BE;(Ⅱ)求平面ACS的法向量为
 ,平面ASD的一个法向量为
,平面ASD的一个法向量为 ,计算
,计算 ,求出二面角C-AS-D的余弦值.
,求出二面角C-AS-D的余弦值.点评:本题考查点、线、面间的距离计算,直线与平面垂直的判定,直线与平面垂直的性质,考查空间想象能力,逻辑思维能力,利用空间直角坐标系,解答立体几何问题,可以说是有一定的规律,要求比较高,不允许出错.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.