题目内容
已知 ,且方程
,且方程 无实数根,下列命题:
无实数根,下列命题:
①方程 也一定没有实数根;
也一定没有实数根;
②若 ,则不等式
,则不等式 对一切实数
对一切实数 都成立;
都成立;
③若 ,则必存在实数
,则必存在实数 ,使
,使
④若 ,则不等式
,则不等式 对一切实数
对一切实数 都成立.
都成立.
其中正确命题的序号是 .
①②④
解析试题分析:根据题意,由于 ,且方程
,且方程 无实数根,
无实数根,
则对于①方程 也一定没有实数根;利用反证法可知成立。
也一定没有实数根;利用反证法可知成立。
对于②若 ,则不等式
,则不等式 对一切实数
对一切实数 都成立;结合二次函数图象与性质可知成立。
都成立;结合二次函数图象与性质可知成立。
对于③若 ,则必存在实数
,则必存在实数 ,使
,使 ,不存在,故错误。
,不存在,故错误。
对于④若 ,则不等式
,则不等式 对一切实数
对一切实数 都成立,结合不等式的思想可知成立故答案为①②④
都成立,结合不等式的思想可知成立故答案为①②④
考点:函数与方程
点评:主要是考查了函数与方程根的问题的运用,属于基础题。

练习册系列答案
相关题目
 的定义域是 ___________.
的定义域是 ___________. ,其中
,其中 为常数,且
为常数,且 .若
.若 为常数,则
为常数,则 的值__________
的值__________ 为R上的偶函数,且当
为R上的偶函数,且当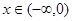 时,
时, ,则当
,则当 时,
时, ___________.
___________. 的值域为___________.
的值域为___________. ,且
,且 为奇函数,则
为奇函数,则 .
. 满足
满足 ,且
,且 时,
时, ,则函数
,则函数 的图象与函数
的图象与函数 图象的交点个数为__________。
图象的交点个数为__________。 是定义在R上的奇函数,当x≤0时,
是定义在R上的奇函数,当x≤0时, ,则
,则 .
. =
= 上是减函数,则
上是减函数,则 的取值范围是___________;
的取值范围是___________;