题目内容
设等差数列{an}的前n项和Sn=n2+bn+c,a1=3,则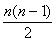 .
.
分析:本题考查数列{an}的通项an与它的前n项和Sn的关系、数列极限的求法等知识点.
解:∵{an}是等差数列,
∴Sn=na1+![]() d=
d=![]() n2+(a1-
n2+(a1-![]() )n.
)n.
又∵Sn=n2+bn+c,∴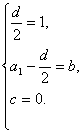
又∵a1=3,∴d=2,b=2,c=0.
∴Sn=n2+2n,an=3+2(n-1)=2n+1.
∴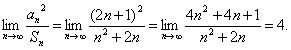
答案:4

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目