题目内容
已知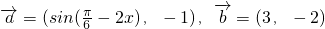 ,且函数
,且函数 ,
,
(1)求f(x)的增区间;
(2)求f(x)在区间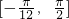 上的最大、最小值及相应的x值.
上的最大、最小值及相应的x值.
解:(1)∵f(x)= •
•
=3sin( -2x)+2
-2x)+2
=-3sin(2x- )+2,
)+2,
∴由2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ (k∈Z)可求其递增区间为:[kπ+
(k∈Z)可求其递增区间为:[kπ+ ,kπ+
,kπ+ ](k∈Z).
](k∈Z).
(2)∵- ≤x≤
≤x≤ ,
,
∴- ≤2x-
≤2x- ≤
≤ ,
,
∵g(x)=-sinx在[- ,
, ]上单调递减,[
]上单调递减,[ ,
, ]上单调递增;
]上单调递增;
∴g(x)max=g(- )=
)= ,由2x-
,由2x- =-
=- 得,x=-
得,x=- ;
;
g(x)min=g( )=-1,由2x-
)=-1,由2x- =
= 得,x=
得,x= .
.
∴当x=- ,f(x)max=3×
,f(x)max=3× +2=
+2= +2;
+2;
当x= 时,f(x)min=3×(-1)+2=-1.
时,f(x)min=3×(-1)+2=-1.
分析:(Ⅰ)由题意可求得f(x)= •
• =-3sin(2x-
=-3sin(2x- )+2,从而可求得f(x)的增区间;
)+2,从而可求得f(x)的增区间;
(Ⅱ)由- ≤x≤
≤x≤ 可求得-
可求得- ≤2x-
≤2x- ≤0,利用正弦函数的性质可求得f(x)在区间
≤0,利用正弦函数的性质可求得f(x)在区间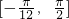 上的最大、最小值及相应的x值.
上的最大、最小值及相应的x值.
点评:本题考查正弦函数的单调性,以向量的数量积为载体考查正弦函数的定义域和值域,求得f(x)=-3sin(2x- )+2是解决问题的关键,属于中档题.
)+2是解决问题的关键,属于中档题.
 •
•
=3sin(
 -2x)+2
-2x)+2=-3sin(2x-
 )+2,
)+2,∴由2kπ+
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ (k∈Z)可求其递增区间为:[kπ+
(k∈Z)可求其递增区间为:[kπ+ ,kπ+
,kπ+ ](k∈Z).
](k∈Z).(2)∵-
 ≤x≤
≤x≤ ,
,∴-
 ≤2x-
≤2x- ≤
≤ ,
,∵g(x)=-sinx在[-
 ,
, ]上单调递减,[
]上单调递减,[ ,
, ]上单调递增;
]上单调递增;∴g(x)max=g(-
 )=
)= ,由2x-
,由2x- =-
=- 得,x=-
得,x=- ;
;g(x)min=g(
 )=-1,由2x-
)=-1,由2x- =
= 得,x=
得,x= .
.∴当x=-
 ,f(x)max=3×
,f(x)max=3× +2=
+2= +2;
+2;当x=
 时,f(x)min=3×(-1)+2=-1.
时,f(x)min=3×(-1)+2=-1.分析:(Ⅰ)由题意可求得f(x)=
 •
• =-3sin(2x-
=-3sin(2x- )+2,从而可求得f(x)的增区间;
)+2,从而可求得f(x)的增区间;(Ⅱ)由-
 ≤x≤
≤x≤ 可求得-
可求得- ≤2x-
≤2x- ≤0,利用正弦函数的性质可求得f(x)在区间
≤0,利用正弦函数的性质可求得f(x)在区间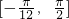 上的最大、最小值及相应的x值.
上的最大、最小值及相应的x值.点评:本题考查正弦函数的单调性,以向量的数量积为载体考查正弦函数的定义域和值域,求得f(x)=-3sin(2x-
 )+2是解决问题的关键,属于中档题.
)+2是解决问题的关键,属于中档题. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,且函数
,且函数 ,
,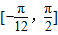 上的最大、最小值及相应的x值;
上的最大、最小值及相应的x值; ,且函数
,且函数 ,
, 上的最大、最小值及相应的x值.
上的最大、最小值及相应的x值.