题目内容
在△ABC中,a、b、c分别是角A、B、C所对的边,B=
,BC=
,AB=1,则△ABC的面积S= .
| π |
| 3 |
| 3 |
考点:正弦定理
专题:解三角形
分析:利用三角形的面积的计算公式即可得出.
解答:
解:△ABC的面积S=
acsinB=
×
×1×sin
=
,
故答案为:
.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 3 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查了三角形的面积的计算公式,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
抛物线x2=-y的准线方程是( )
| A、4x-1=0 |
| B、4y-1=0 |
| C、2x-1=0 |
| D、2y-1=0 |
函数f(x)=x+
在区间[1,3]上的最小值是( )
| 4 |
| x |
| A、3 | ||
| B、5 | ||
| C、4 | ||
D、
|
已知x1是方程xlgx=2010的根,x2是方程x•10x=2010的根,则x1•x2=( )
| A、20102 |
| B、2010 |
| C、20112 |
| D、2011 |
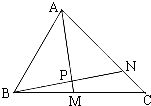 如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN交于点P,求AP:PM与BP:PN的值.
如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN交于点P,求AP:PM与BP:PN的值.