题目内容
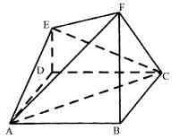
已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
解析:
如图,连结EG、FG、EF、BD、AC、EF、BD分别交AC于H、O. 因为ABCD是正方形,E、F分别为AB和AD的中点,故EF∥BD,H为AO的中点.
BD不在平面EFG上.否则,平面EFG和平面ABCD重合,从而点G在平面的ABCD上,与题设矛盾.
由直线和平面平行的判定定理知BD∥平面EFG,所以BD和平面EFG的距离就是点B到平面EFG的距离. ——4分
 ∵ BD⊥AC,
∵ BD⊥AC,
∴ EF⊥HC.
∵ GC⊥平面ABCD,
∴ EF⊥GC,
∴ EF⊥平面HCG.
∴ 平面EFG⊥平面HCG,HG是这两个垂直平面的交线. ——6分
作OK⊥HG交HG于点K,由两平面垂直的性质定理知OK⊥平面EFG,所以线段OK的长就是点B到平面EFG的距离. ——8分
∵ 正方形ABCD的边长为4,GC=2,
∴ AC=4![]() ,HO=
,HO=![]() ,HC=3
,HC=3![]() .
.
∴ 在Rt△HCG中,HG=![]() .
.
由于Rt△HKO和Rt△HCG有一个锐角是公共的,故Rt△HKO∽△HCG.
∴ OK=![]() .
.
即点B到平面EFG的距离为![]() . ——10分
. ——10分
注:未证明“BD不在平面EFG上”不扣分.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2. 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.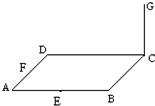 已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离. 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.