题目内容
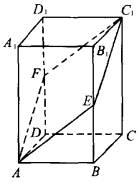
如图所示的正四棱柱ABCD—A1B
(1)异面直线CE与AF所成的角;
(2)A
(3)二面角B—A
解:如图,以D为原点,DA为Ox轴正方向,DC为Oy轴正方向,DD1为Oz轴正方向建立空间直角坐标系.?

∵A![]() =(1,-1,4),
=(1,-1,4),![]() =(-1,2,2),
=(-1,2,2),![]() =(-1,2,-2),
=(-1,2,-2),![]() =(-1,0,-2),
=(-1,0,-2),![]() =(0,0,-4),
=(0,0,-4),![]() =(1,1,-4).?
=(1,1,-4).?
(1)设异面直线CE和AF所成的角为α,则 ?
cosα=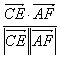 =
=![]() =
=![]() ,?
,?
∴α=arccos![]() ,此即异面直线CE和AF所成的角.?
,此即异面直线CE和AF所成的角.?
(2)∵A1B1⊥平面BCC1B1,?
∴A
则cosβ=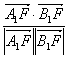 ?
?
=![]() =
=![]() .?
.?
∴β=arccos![]() .?
.?
此即为A
(3)∵EB⊥A
则cosγ= =
=![]() =
=![]() ,?
,?
∴γ=arccos![]() .?
.?
此即为所求二面角B—A

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
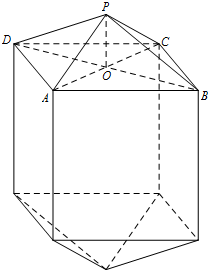 某公司拟制造如图所示的工件(长度单位:米),要求工件的体积为10立方米,其中工件的中间为长方体,上下两端为相同的正四棱锥,其底面边长AB=a,高PO=
某公司拟制造如图所示的工件(长度单位:米),要求工件的体积为10立方米,其中工件的中间为长方体,上下两端为相同的正四棱锥,其底面边长AB=a,高PO= 一个三棱柱恰好可放入一个正四棱柱的容体中,底面如图所示,其中三棱柱的底面AEF是一个直角三角形,∠AEF=90°,AE=a,EF=b,三棱柱的高与正四棱柱的高均为1,则此正四棱柱的体积为
一个三棱柱恰好可放入一个正四棱柱的容体中,底面如图所示,其中三棱柱的底面AEF是一个直角三角形,∠AEF=90°,AE=a,EF=b,三棱柱的高与正四棱柱的高均为1,则此正四棱柱的体积为