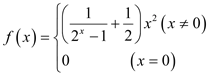题目内容
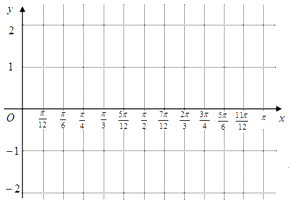
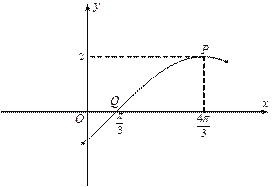
【题目】如图为函数![]() 图像的一部分,其中点
图像的一部分,其中点![]() 是图像的一个最高点,点
是图像的一个最高点,点![]() 是与点
是与点![]() 相邻的图像与
相邻的图像与![]() 轴的一个交点.
轴的一个交点.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若将函数![]() 的图像沿
的图像沿![]() 轴向右平移
轴向右平移![]() 个单位,再把所得图像上每一点的横坐标都变为原来的
个单位,再把所得图像上每一点的横坐标都变为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递增区间.
的单调递增区间.
【答案】(1) ![]() ⑵
⑵![]()
【解析】试题分析:(1)由函数![]() 的图象求出
的图象求出![]() 和
和![]() 的值,写出
的值,写出![]() 的解析式;
的解析式;
(2)根据函数图象平移法则,写出平移后的函数解析式,求出它的单调增区间.
试题解析:
(1)由图像可知![]() ,
,
又![]() ,
, ![]() ,
, ![]() ,
,
又![]() 点
点![]() 是函数图像
是函数图像![]() 的一个最高点,
的一个最高点,
则![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
故![]()
⑵由⑴得, ![]() ,
,
把函数![]() 的图像沿
的图像沿![]() 轴向右平移
轴向右平移![]() 个单位,
个单位,
得到![]() ,
,
再把所得图像上每一点的横坐标都变为原来的![]() (纵坐标不变),
(纵坐标不变),
得到![]() ,
,
由![]() 得
得![]() ,
,
∴![]() 的单调增区间是
的单调增区间是![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目