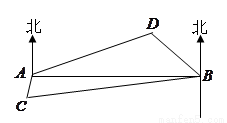题目内容
 如图,A,B是海面上位于东西方向相距10(3+
如图,A,B是海面上位于东西方向相距10(3+| 3 |
| 3 |
分析:先根据内角和求得∠DAB和,∠DBA及进而求得∠ADB,在△ADB中利用正弦定理求得DB的长,进而利用里程除以速度即可求得时间.
解答: 解:由题意知AB=10(3+
解:由题意知AB=10(3+
)海里,BC=40
海里
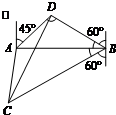
∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°,
在△ADB中,有正弦定理得
=
∴DB=
=
=20
又在△DBC中,∠DBC=60°
DC2=DB2+BC2-2×DB×BC×cos600
1200+4800-2×20
×40
×
=3600
∴DC=60.
∴救援船到达D点需要的时间为
=2(小时)
答:该救援船到达D点需要2小时.
 解:由题意知AB=10(3+
解:由题意知AB=10(3+| 3 |
| 3 |
∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°,
在△ADB中,有正弦定理得
| DB |
| sin∠DAB |
| AB |
| sin∠ADB |
∴DB=
| AB•sin∠DAB |
| sin∠ADB |
=
10(3+
| ||
| sin105° |
| 3 |
又在△DBC中,∠DBC=60°
DC2=DB2+BC2-2×DB×BC×cos600
1200+4800-2×20
| 3 |
| 3 |
| 1 |
| 2 |
∴DC=60.
∴救援船到达D点需要的时间为
| 60 |
| 30 |
答:该救援船到达D点需要2小时.
点评:本题主要考查了解三角形的实际应用.考查了学生运用所学知识解决实际问题的能力.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意余弦定理和数形结合思想的灵活运用.

练习册系列答案
相关题目
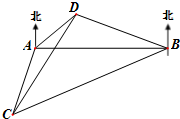 如图,A,B是海面上位于东西方向相距5(3+
如图,A,B是海面上位于东西方向相距5(3+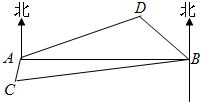 如图,A,B是海面上位于东西方向相距5(3+
如图,A,B是海面上位于东西方向相距5(3+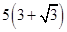 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距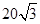 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?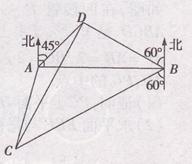
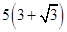 海里的两个观测点,现位于A点北偏东60°,B点北偏西45°的D点有一艘轮船发出求救信号,位于B点南偏西75°且与B点相距
海里的两个观测点,现位于A点北偏东60°,B点北偏西45°的D点有一艘轮船发出求救信号,位于B点南偏西75°且与B点相距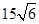 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?