题目内容
【题目】(12分)如图,椭圆![]() (
(![]() )的离心率
)的离心率![]() ,短轴的两个端点分别为B1、B2,焦点为F1、F2,四边形F1 B1F2 B2的内切圆半径为
,短轴的两个端点分别为B1、B2,焦点为F1、F2,四边形F1 B1F2 B2的内切圆半径为![]()
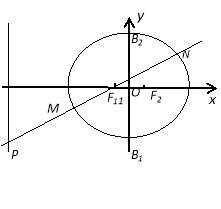
(1)求椭圆C的方程;
(2)过左焦点F1的直线交椭圆于M、N两点,交直线![]() 于点P,设
于点P,设![]() ,
,![]() ,试证
,试证![]() 为定值,并求出此定值.
为定值,并求出此定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题解析:(1)设四边形F1B1F2B2的内切圆与边B1B2的切点为G,连接OG,则|OG|=![]()
由S△OB2F2=![]() |OB2||OF2|=
|OB2||OF2|=![]() |B2F2||OG|,|OB2|=b, |OF2|=c, |B2F2|=a,得bc=
|B2F2||OG|,|OB2|=b, |OF2|=c, |B2F2|=a,得bc=![]() a
a
又∵e=![]()
解得a=2,b=![]()
故椭圆方程为:![]()
(2)设直线MN的方程为y=k(x+1)代入椭圆方程,整理得
(3+4k2)x2+8k2x+4(k2-3)=0
设M(x1,y1),N(x2,y2), 则x1+ x2=![]() ,x1x2=
,x1x2=![]()
又P(-4,-3k),F2(-1,0)
由![]() ,
, ![]() 得
得
![]() ,
,![]()
∴![]()
![]()
∵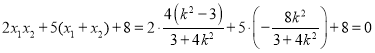
∴![]() 为定值
为定值

练习册系列答案
相关题目