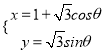题目内容
【题目】已知椭圆C1: ![]() (a>b>0)的离心率为e=
(a>b>0)的离心率为e=![]() ,过C1的左焦点F1的直线l:x-y+2=0,直线l被圆C2:
,过C1的左焦点F1的直线l:x-y+2=0,直线l被圆C2: ![]() +
+![]() =
=![]() (r>0)截得的弦长为2
(r>0)截得的弦长为2![]() .
.
(1)求椭圆C1的方程:
(2)设C1的右焦点为F2,在圆C2上是否存在点P,满足|PF1|=![]() |PF2|,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
|PF2|,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
【答案】(1)![]() (2)不存在
(2)不存在
【解析】试题分析:(I)求出F1点坐标即可得出c,进而利用离心率得出a,b,求出椭圆方程;
(II)利用垂径定理求出圆C2的半径r,根据|PF1|=![]() |PF2|列方程求出P点轨迹方程,根据轨迹与圆C2有无交点得出结论.
|PF2|列方程求出P点轨迹方程,根据轨迹与圆C2有无交点得出结论.
试题解析:
(Ⅰ)直线与x轴的交点坐标为(﹣2,0),∴F1(﹣2,0).
即c=2,又e=![]() =
=![]() ,∴a=4,b=
,∴a=4,b=![]() =2
=2![]() ,
,
∴椭圆C1的方程为![]() .
.
(Ⅱ)∵圆心C2(3,3)到直线l的距离d=![]() =
=![]() ,
,
又直线l被圆C2截得的弦长为2![]() ,
,
∴圆C2的半径r=![]() =2,
=2,
故圆C2的方程为(x﹣3)2+(y﹣3)2=4.
设圆C2上存在点P(x,y),满足|PF1|=![]() |PF2|,即|PF1|=
|PF2|,即|PF1|=![]() |PF2|,
|PF2|,
又F1(﹣2,0),F2(2,0),∴![]() ,
,
整理得(x﹣14)2+y2=192,表示圆心在C(14,0),半径是8![]() 的圆.
的圆.
∴|CC2|=![]() ,
,
∴两圆没有公共点.
∴圆C2上不存在点P满足|PF1|=![]() |PF2|.
|PF2|.

练习册系列答案
相关题目