题目内容
若f(x)≥h(x)=ax+b≥g(x),则定义h(x)为曲线f(x),g(x)的φ线.已知f(x)=tanx,x∈[0,
| π |
| 2 |
| π |
| 2 |
分析:如图,在直角坐标系中做出单位圆,利用三角形POA的面积 小于扇形 AOP的面积,而扇形 AOP的面积小于直角三角形 OAT 的面积,可得 sinx<x<tanx,故 h(x)=x 满足条件.
解答: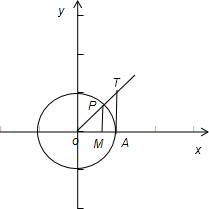 解:∵x∈[0,
解:∵x∈[0,
),设角x的终边为OP,
P是角x的终边与单位圆的交点,角x的余弦线为OM,正弦线 MP,
正切线 AT,由于三角形POA的面积 小于扇形AOP的面积,
而扇形 AOP的面积小于直角三角形 OAT 的面积,
∴
×1×PM<
•x•12<
×AT,∴MP<x<AT,
∴sinx<x<tanx,故 h(x)=x 满足条件,故答案为y=x.
 解:∵x∈[0,
解:∵x∈[0,| π |
| 2 |
P是角x的终边与单位圆的交点,角x的余弦线为OM,正弦线 MP,
正切线 AT,由于三角形POA的面积 小于扇形AOP的面积,
而扇形 AOP的面积小于直角三角形 OAT 的面积,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴sinx<x<tanx,故 h(x)=x 满足条件,故答案为y=x.
点评:本题考查单位圆中胡三角函数线的定义,利用三角形POA的面积 小于扇形 AOP的面积,而扇形 AOP的面积小于直角三角形 OAT 的面积.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
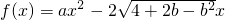 ,
,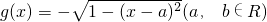 .
.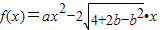 ,
,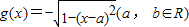 .
. ,
, .
.