题目内容
已知数列{an}中,a1=8,a4=2满足an+2-2an+1+an=0(n∈N*),
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn;
(3)设bn=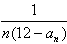 ,Tn=b1+b2+…+bn(n∈N*)是否存在最大的整数m,使得对任意n∈N*,均有
,Tn=b1+b2+…+bn(n∈N*)是否存在最大的整数m,使得对任意n∈N*,均有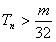 成立?若存在,求出m,若不存在,请说明理由。
成立?若存在,求出m,若不存在,请说明理由。
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn;
(3)设bn=
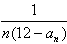 ,Tn=b1+b2+…+bn(n∈N*)是否存在最大的整数m,使得对任意n∈N*,均有
,Tn=b1+b2+…+bn(n∈N*)是否存在最大的整数m,使得对任意n∈N*,均有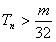 成立?若存在,求出m,若不存在,请说明理由。
成立?若存在,求出m,若不存在,请说明理由。 解:(1) ;
;
(2)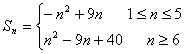 ;
;
(3)由(1)可得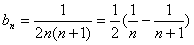 ,
,
则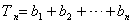
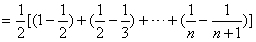
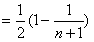 ,
,
由Tn为关于n的增函数,
故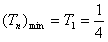 ,
,
于是欲使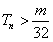 对n∈N*恒成立,则
对n∈N*恒成立,则 ,则m<8,
,则m<8,
∴存在最大的整数m=7满足题意。
 ;
;(2)
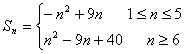 ;
;(3)由(1)可得
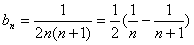 ,
,则
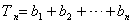
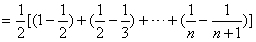
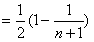 ,
,由Tn为关于n的增函数,
故
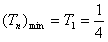 ,
,于是欲使
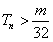 对n∈N*恒成立,则
对n∈N*恒成立,则 ,则m<8,
,则m<8,∴存在最大的整数m=7满足题意。

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|