Question

半径分别为1,3的两圆相外切,则外公切线的两切点与两圆相切的切点所围成三角形的面积为（    ）

A.1                  B.2                     C.                 D.

Answer 1

解析：如图，设⊙O₁、⊙O₂外切于点D，公切线AB的切点为A、B，过点O₁作O₁C⊥O₂B于C，则∠CO₁O₂=30°，O₁O₂=4，O₂C=2，O₁C=2.

又∵∠O₂=60°，∴∠O₁=120°.

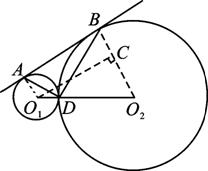
∴DB=O₂ B=3，AD=.

∴S_△ABD=AD·DB=××3=.故选D.

答案:D