Question

设直线l与球O有且只有一个公共点P，从直线l出发的两个半平面α，β截球O的两个截面圆的半径分别为1和

3

，二面角α-l-β的平面角为

5π

6

，则球O的表面积等于

 

．

Answer 1

分析：过P与O作直线l的垂面，画出截面图形，设出球的半径，通过解三角形，利用转化思想求出球的半径的平方，然后求出球的表面积．

解答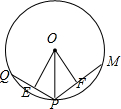：解：过P与O作直线l的垂面，画出截面图形，如图
设球的半径为r，作OE⊥QP，OF⊥PM，则EP=1，PF=

3

，
设∠OPE=α，∠OPF=

5π

6

-α，
所以

rcosα

rcos( 5π 6 -α)

=

1

3

，
即sinα=3

3

cosα，sin²α+cos²α=1解得
cos²α=

1

28

所以r²=

1

cos2α

；
所以球的表面积为：4πr²=4π×28=112π．
故答案为112π．

点评：本题是中档题，考查二面角的有关知识，考查转化思想的应用，空间想象能力，计算能力．