题目内容
y=f(x)是关于x=3对称的奇函数,f(1)=1,cosx-sinx=
,则f[
]=
3
| ||
| 5 |
| 15sin2x | ||
cos(x+
|
-1
-1
.分析:由题意,可由cosx-sinx=
先化简
,解出它的值为7,再由y=f(x)是关于x=3对称的奇函数,f(1)=1,即可得到f(7)=f(-1)=-f(1),函数值可求得.
3
| ||
| 5 |
| 15sin2x | ||
cos(x+
|
解答:解:由题意cosx-sinx=
,可得1-2cosxsinx=
,可得sin2x=
又可得cos(x+
)=
(cosx-sinx)=
∴
=
=7
又y=f(x)是关于x=3对称的奇函数,f(1)=1
∴f(7)=f(-1)=-f(1)=-1
故答案为-1
3
| ||
| 5 |
| 18 |
| 25 |
| 7 |
| 25 |
又可得cos(x+
| π |
| 4 |
| ||
| 2 |
| 3 |
| 5 |
∴
| 15sin2x | ||
cos(x+
|
15×
| ||
|
又y=f(x)是关于x=3对称的奇函数,f(1)=1
∴f(7)=f(-1)=-f(1)=-1
故答案为-1
点评:本题考查二倍角的正弦,余弦的和角公式,函数的奇偶性与对称性,解题的关键是理解题意,综合利用题设条件求值,本题的难点有二,一是求
的值,二是由函数的性质将
的函数值用1的函数值表示出来,本题考查了推理判断的能力,根据公式计算的能力,考查了转化的思想,是函数与三角结合的综合题,解题时知识转换快,要严谨.
| 15sin2x | ||
cos(x+
|
| 15sin2x | ||
cos(x+
|

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
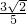 ,若t=
,若t=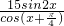 ,则f(t)=________.
,则f(t)=________.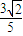 ,若t=
,若t=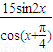 ,则f(t)= .
,则f(t)= .