题目内容
关于x的方程x2•log
a-2x+1=0有实数根,则a的取值范围是( )
| 1 |
| 2 |
A、a≤
| ||
B、a≥
| ||
C、0<a≤
| ||
D、
|
分析:对于x2前面有参数的方程首先考虑参数等于0的情况,当log
a=0时,可求出a=1然后验证此时方程有实数根满足条件,即可进而可排除A、C、D,得到答案.
| 1 |
| 2 |
解答:解:当a=1时,关于x的方程x2•log
a-2x+1=0转化为-2x+1=0,
可得到x=
,方程有实数根,故当a=1满足条件,
排除A、C、D.
故选B.
| 1 |
| 2 |
可得到x=
| 1 |
| 2 |
排除A、C、D.
故选B.
点评:本题主要考查含参数的一元二次方程根的判断.对于这种题型首先要考虑的是二次项系数等于0的情况,其次再根据二次函数或方程的有关性质进行解题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
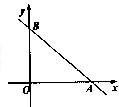 如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.
如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.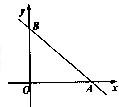 如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.
如图直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2-14x+4(AB+2)=0的两个根(OA<OB),P为直线l上异于A、B两点之间的一动点. 且PQ∥OB交OA于点Q.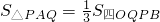 时,请你确定P点在AB上的位置,并求出线段PQ的长;
时,请你确定P点在AB上的位置,并求出线段PQ的长;