题目内容
给出下列说法:
①命题“若α= ,则sinα=
,则sinα= ”的否命题是假命题;
”的否命题是假命题;
②命题p:?x∈R,使sinx>1,则 p:?x∈R,sinx≤1;
p:?x∈R,sinx≤1;
③“φ= +2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件;
+2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件;
④命题p:?x∈(0, ),使sinx+cosx=
),使sinx+cosx= ,命题q:在△ABC中,若sinA>sinB,则A>B,那么命题(
,命题q:在△ABC中,若sinA>sinB,则A>B,那么命题( p)∧q为真命题.
p)∧q为真命题.
其中正确的个数是( )
①命题“若α=
 ,则sinα=
,则sinα= ”的否命题是假命题;
”的否命题是假命题;②命题p:?x∈R,使sinx>1,则
 p:?x∈R,sinx≤1;
p:?x∈R,sinx≤1;③“φ=
 +2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件;
+2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件;④命题p:?x∈(0,
 ),使sinx+cosx=
),使sinx+cosx= ,命题q:在△ABC中,若sinA>sinB,则A>B,那么命题(
,命题q:在△ABC中,若sinA>sinB,则A>B,那么命题( p)∧q为真命题.
p)∧q为真命题.其中正确的个数是( )
| A.4 | B.3 | C.2 | D.1 |
B
①中命题的否命题是“若α≠ ,则sinα≠
,则sinα≠ ”这个命题是假命题,如α=
”这个命题是假命题,如α= 时,sinα=
时,sinα= ,故说法①正确;根据对含有量词的命题否定的方法,说法②正确;说法③中函数y=sin(2x+φ)为偶函数
,故说法①正确;根据对含有量词的命题否定的方法,说法②正确;说法③中函数y=sin(2x+φ)为偶函数 sin(-2x+φ)=sin(2x+φ)
sin(-2x+φ)=sin(2x+φ)  cosφsin2x=0对任意x恒成立
cosφsin2x=0对任意x恒成立 cosφ=0
cosφ=0 φ=kπ+
φ=kπ+ (k∈Z),所以y=sin(2x+φ)为偶函数的充要条件是φ=kπ+
(k∈Z),所以y=sin(2x+φ)为偶函数的充要条件是φ=kπ+ (k∈Z),说法③不正确;当x∈(0,
(k∈Z),说法③不正确;当x∈(0, )时,恒有sinx+cosx>1,故命题p为假命题,
)时,恒有sinx+cosx>1,故命题p为假命题, p为真命题,根据正弦定理sinA>sinB
p为真命题,根据正弦定理sinA>sinB 2RsinA>2RsinB
2RsinA>2RsinB a>b
a>b A>B,命题q为真命题,故(
A>B,命题q为真命题,故( p)∧q为真命题,说法④正确.
p)∧q为真命题,说法④正确.
 ,则sinα≠
,则sinα≠ ”这个命题是假命题,如α=
”这个命题是假命题,如α= 时,sinα=
时,sinα= ,故说法①正确;根据对含有量词的命题否定的方法,说法②正确;说法③中函数y=sin(2x+φ)为偶函数
,故说法①正确;根据对含有量词的命题否定的方法,说法②正确;说法③中函数y=sin(2x+φ)为偶函数 sin(-2x+φ)=sin(2x+φ)
sin(-2x+φ)=sin(2x+φ)  cosφsin2x=0对任意x恒成立
cosφsin2x=0对任意x恒成立 cosφ=0
cosφ=0 φ=kπ+
φ=kπ+ (k∈Z),所以y=sin(2x+φ)为偶函数的充要条件是φ=kπ+
(k∈Z),所以y=sin(2x+φ)为偶函数的充要条件是φ=kπ+ (k∈Z),说法③不正确;当x∈(0,
(k∈Z),说法③不正确;当x∈(0, )时,恒有sinx+cosx>1,故命题p为假命题,
)时,恒有sinx+cosx>1,故命题p为假命题, p为真命题,根据正弦定理sinA>sinB
p为真命题,根据正弦定理sinA>sinB 2RsinA>2RsinB
2RsinA>2RsinB a>b
a>b A>B,命题q为真命题,故(
A>B,命题q为真命题,故( p)∧q为真命题,说法④正确.
p)∧q为真命题,说法④正确.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
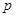 : 关于
: 关于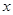 的不等式
的不等式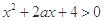 ,对一切
,对一切 恒成立; 命题
恒成立; 命题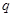 : 函数
: 函数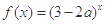 在
在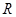 上是增函数.若
上是增函数.若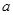 的取值范围.
的取值范围.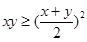 的充要条件
的充要条件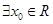 ,
,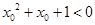 则
则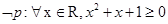
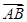 ·
·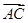 =
=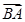 ·
·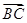 ,则|
,则| ,则
,则 ”的否命题为 .
”的否命题为 . :
: ,则( )
,则( )


