题目内容
已知函数
(1)求函数f(x)的定义域
(2)证明函数f(x)在(-∞,0)上为减函数.
解:(1)
又∵2x-1≠0?x≠0,
∴函数f(x)的定义域{x|x∈R且x≠0},
(2)设x1,x2∈(-∞,0)且x1<x2
则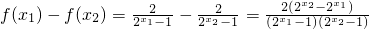 ,
,
∵x1,x2∈(-∞,0)且x1<x2,
∴ 且
且 ,
,
∴ >0
>0
∴f(x1)-f(x2)>0,
即f(x1)>f(x2)
∴根据函数单调性的定义知:函数f(x)在(-∞,0)上为减函数.
分析:(1)要是函数有意义,只需函数分母不为零即可,解这个指数不等式即可得函数的定义域;
(2)利用函数单调性的定义,设x1,x2∈(-∞,0)且x1<x2,利用作差法证明f(x1)>f(x2),进而证明函数f(x)在(-∞,0)上为减函数
点评:本题主要考查了函数定义域的求法,函数单调性的定义,证明函数单调性的方法,指数不等式的解法与指数函数的单调性的应用,属基础题

又∵2x-1≠0?x≠0,
∴函数f(x)的定义域{x|x∈R且x≠0},
(2)设x1,x2∈(-∞,0)且x1<x2
则
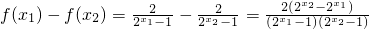 ,
,∵x1,x2∈(-∞,0)且x1<x2,
∴
 且
且 ,
,∴
 >0
>0∴f(x1)-f(x2)>0,
即f(x1)>f(x2)
∴根据函数单调性的定义知:函数f(x)在(-∞,0)上为减函数.
分析:(1)要是函数有意义,只需函数分母不为零即可,解这个指数不等式即可得函数的定义域;
(2)利用函数单调性的定义,设x1,x2∈(-∞,0)且x1<x2,利用作差法证明f(x1)>f(x2),进而证明函数f(x)在(-∞,0)上为减函数
点评:本题主要考查了函数定义域的求法,函数单调性的定义,证明函数单调性的方法,指数不等式的解法与指数函数的单调性的应用,属基础题

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线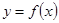 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)