题目内容
已知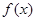 是定义在
是定义在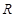 上的奇函数,当
上的奇函数,当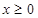 时,
时,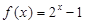 .
.
(1)求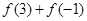 ;
;
(2)求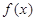 的解析式;
的解析式;
(3)若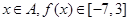 ,求区间
,求区间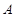 .
.
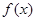 是定义在
是定义在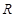 上的奇函数,当
上的奇函数,当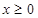 时,
时,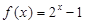 .
.(1)求
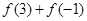 ;
;(2)求
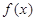 的解析式;
的解析式;(3)若
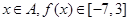 ,求区间
,求区间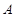 .
.(1) ;(2)
;(2) ;(3)区间
;(3)区间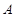 为
为 .
.
 ;(2)
;(2) ;(3)区间
;(3)区间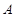 为
为 .
.试题分析:(1) ∵
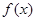 是奇函数,,∴
是奇函数,,∴ ,∴
,∴ ,
,∴
 ;
;(2)只需要求出
 的解析式即可,利用奇函数
的解析式即可,利用奇函数 ,所以设
,所以设 ,则
,则 ,则
,则 ,再与
,再与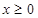 的解析式和在一起,写出分段函数;
的解析式和在一起,写出分段函数;(3)本题是已知函数的值域求定义域问题,根据函数图象可得
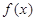 在
在 上单调递增,分别讨论
上单调递增,分别讨论 ,
,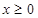 来求解,当
来求解,当 时,
时, 解得
解得 ;当
;当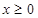 时,
时, 解得
解得 ;所以区间
;所以区间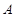 为
为 .
.试题解析:(1)∵
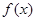 是奇函数,
是奇函数,∴
 3分
3分(2)设
 ,则
,则 ,∴
,∴
∵
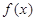 为奇函数,∴
为奇函数,∴ 5分
5分∴
 6分
6分(3)根据函数图象可得
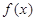 在
在 上单调递增 7分
上单调递增 7分当
 时,
时, 解得
解得 9分
9分当
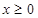 时,
时, 解得
解得 11分
11分∴区间
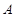 为
为 . 12分
. 12分
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
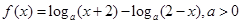 且
且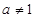 .
.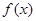 的定义域;
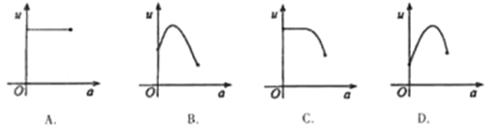
的定义域;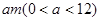 、4m,不考虑树的粗细,现在用16m长的篱笆, 借助墙角围成一个矩形的共圃ABCD,设此矩形花圃的面积为Sm2,S的最大值为
、4m,不考虑树的粗细,现在用16m长的篱笆, 借助墙角围成一个矩形的共圃ABCD,设此矩形花圃的面积为Sm2,S的最大值为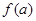 ,若将这棵树围在花圃中,则函数
,若将这棵树围在花圃中,则函数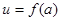 的图象大致是( )
的图象大致是( )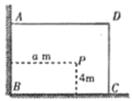
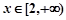 ,使不等式
,使不等式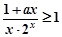 成立,则实数
成立,则实数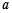 的最小值为 .
的最小值为 .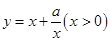 有如下性质:若常数
有如下性质:若常数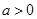 ,则函数在
,则函数在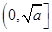 上是减函数,在
上是减函数,在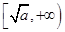 上是增函数。已知函数
上是增函数。已知函数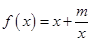 (
(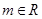 为常数),当
为常数),当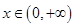 时,若对任意
时,若对任意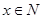 ,都有
,都有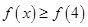 ,则实数
,则实数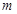 的取值范围是 .
的取值范围是 .



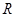 上的函数
上的函数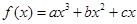
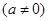 的单调增区间为
的单调增区间为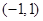 ,若方程
,若方程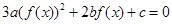 恰有6个不同的实根,则实数
恰有6个不同的实根,则实数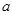 的取值范围是 .
的取值范围是 .