题目内容
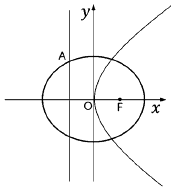
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且椭圆C上的点到椭圆右焦点F的最小距离为
,且椭圆C上的点到椭圆右焦点F的最小距离为 ![]() .
.
(1)求椭圆C的方程;
(2)过点F且不与坐标轴平行的直线l与椭圆C交于A,B两点,线段AB的中点为M, O为坐标原点,直线 ![]() 的斜率分别为
的斜率分别为 ![]() 若成等差数列,求直线l的方程.
若成等差数列,求直线l的方程.
【答案】
(1)解: 点F的坐标为 ![]() ,由题意可得:
,由题意可得: 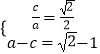
得 ![]()
∴椭圆C的方程为 ![]()
(2)解: 设点 ![]() ,又
,又 ![]() ,故直线l的方程可设为
,故直线l的方程可设为 ![]() ,
,
由 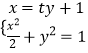 ,得
,得 ![]() ,
,
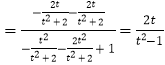 .
.
又  成等差数列,
成等差数列,
![]() ,即
,即 ![]() ,故直线l的方程为
,故直线l的方程为 ![]() ,
,
即 ![]()
【解析】(1)由椭圆的离心率可得出a与c的关系,进而可得出当点位于右顶点时到椭圆右焦点F的最小距离为:a-c=![]() -1,再结合椭圆里
-1,再结合椭圆里![]() 的关系求出a和b的值故得到椭圆的方程。(2)先设出直线l的方程代入椭圆的方程结合韦达定理
的关系求出a和b的值故得到椭圆的方程。(2)先设出直线l的方程代入椭圆的方程结合韦达定理![]() 以及中点坐标的公式,即可求得MP的方程然后求得x0、y0关于t的代数式,再利用直线的斜率成等差数列得到关于t的方程,解出其值就求出了斜率的斜率,再利用直线的斜截式求出直线的方程。
以及中点坐标的公式,即可求得MP的方程然后求得x0、y0关于t的代数式,再利用直线的斜率成等差数列得到关于t的方程,解出其值就求出了斜率的斜率,再利用直线的斜截式求出直线的方程。
【考点精析】认真审题,首先需要了解直线的斜率(一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα).

练习册系列答案
相关题目