题目内容
(本小题满分12分)
在△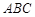 中,点
中,点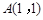 ,
,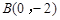 ,
,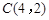 ,
,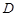 为
为 的中点,
的中点,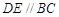 .
.
(Ⅰ)求 边上的高所在直线的方程;
边上的高所在直线的方程;
(Ⅱ)求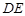 所在直线的方程.
所在直线的方程.
(1)  (2)
(2) 
解析试题分析:解:(Ⅰ)因为 (1,1) ,
(1,1) , (0,-2),
(0,-2), (4,2),
(4,2),
所以 所在直线的斜率为1, ………………………2分
所在直线的斜率为1, ………………………2分
所以 边高所在直线的斜率为-1, …………………4分
边高所在直线的斜率为-1, …………………4分
所以 边高所在直线的方程为
边高所在直线的方程为 ,
,
即 . ………………………6分
. ………………………6分
(Ⅱ)因为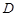 为
为 的中点,所以
的中点,所以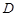
 , ………………………8分
, ………………………8分
又因为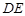 //
// ,
,
所以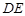 所在直线的方程为
所在直线的方程为 ,
,
即 . ………………………12分
. ………………………12分
考点:本试题考查了直线方程。
点评:解决直线方程的一般就是求解一个点和一个斜率,或者是斜率和截距来得到直线的方程。同时要结合平行系或者垂直直线系的直线方程来求解。属于中档题。

练习册系列答案
相关题目
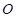 :
: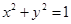 和定点
和定点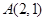 ,由⊙
,由⊙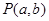 向⊙
向⊙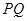 ,切点为
,切点为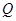 ,且满足
,且满足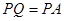 .
.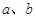 间满足的等量关系;
间满足的等量关系;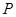 为圆心所作的⊙
为圆心所作的⊙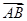 =(4,2).
=(4,2).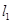 :
: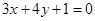 和点
和点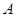 (1,2),设过
(1,2),设过 .
.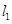 :
: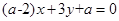 和
和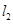 :
: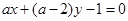 。
。 垂直,并且与原点的距离是5的直线的方程.
垂直,并且与原点的距离是5的直线的方程.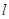 经过直线
经过直线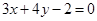 与直线
与直线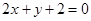 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
.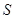 .
. 平
平 行
行