题目内容
若 为正实数且满足
为正实数且满足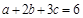 .
.
(1)求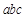 的最大值为
的最大值为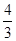 ;(2)求
;(2)求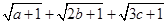 的最大值.
的最大值.
(1)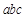 的最大值为
的最大值为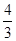 ;(2)
;(2) 的最大值为
的最大值为 .
.
解析试题分析:(1)由已知,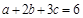 (定值),利用三元均值不等式
(定值),利用三元均值不等式 ,即可求得
,即可求得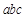 最大值;(2)利用柯西不等式:
最大值;(2)利用柯西不等式: ,当且仅当
,当且仅当 ,即当
,即当 时,等号成立,此时
时,等号成立,此时 取最大值,最后求得
取最大值,最后求得 的最大值.
的最大值.
试题解析:(1) ,
, .
.
当且仅当 即
即 时等号成立.所以
时等号成立.所以 的最大值为
的最大值为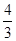 . 3分
. 3分
(2)由柯西不等式, ,当且仅当
,当且仅当 即
即 时等号成立.
时等号成立.
所以 的最大值为
的最大值为 .
. 7分..
7分..
考点:1.利用三元均值不等式求乘积函数的最大值;2.利用利用柯西不等式求函数的最值.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
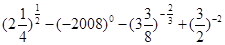
 ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过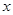 年,树林中有木材
年,树林中有木材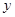
 ,
, )
) 元,
元,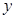 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格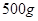 ,按每年
,按每年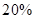 衰减.
衰减.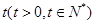 年后,这种放射性元素的质量
年后,这种放射性元素的质量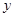 与
与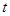 的函数关系式;
的函数关系式;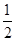 时所经历的时间).(
时所经历的时间).(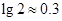 )
)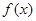 对任意实数
对任意实数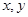 均有
均有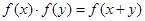 ,且当
,且当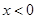 时
时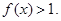
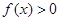 ;
;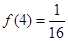 时, 对
时, 对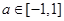 时恒有
时恒有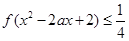 ,求实数
,求实数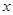 的取值范围.
的取值范围. 在
在 上单调递减且满足
上单调递减且满足 .
. 的取值范围.
的取值范围. ,求
,求 在
在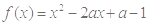 在区间[0,1]上有最小值-2,求
在区间[0,1]上有最小值-2,求 的值.
的值.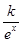 (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.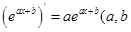 为常数
为常数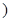 .
.