题目内容
用0,1,2,3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的五位数?
(3)能组成多少个无重复数字且比1325大的四位数?
(1)符合要求的四位偶数可分为三类:
第一类:0在个位时有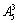 个;
个;
第二类:2在个位时,首位从1,3,4,5中选定1个(有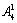 种),十位和百位从余下的数字中选(有
种),十位和百位从余下的数字中选(有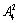 种),于是有
种),于是有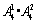 个;
个;
第三类:4在个位时,与第二类同理,也有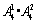 个.
个.
由分类加法计数原理知,共有四位偶数: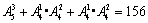 个.
个.
(2)符合要求的五位数中5的倍数的数可分为两类:个位数上的数字是0的五位数有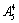 个;个位数上的数字是5的五位数有
个;个位数上的数字是5的五位数有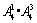 个.故满足条件的五位数的个数共有
个.故满足条件的五位数的个数共有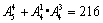 个.
个.
(3)符合要求的比1325大的四位数可分为三类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共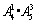 个;
个;
第二类:形如14□□,15□□,共有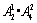 个;
个;
第三类:形如134□,135□,共有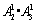 个;
个;
由分类加法计数原理知,无重复数字且比1325大的四位数共有:
 个.
个.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
中、印两国争夺某项国际博览会的申办权,进入最后一道程序,由国际展览局三名执委投票,决定承办权的最后归属。资料显示,A,B,C三名执委投票意向如下表所示
|
| 中 国 | 印度 |
| A |
|
|
| B |
|
|
| C |
|
|
规定每位执委只有一票,且不能弃权,已知中国获得两票的概率为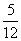 。
。
(1)求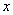 ,
,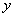 的值;
的值;
(2)设中国获得的票数为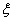 ,试写出
,试写出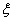 的概率分布列,并求E
的概率分布列,并求E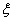 。
。





 (n
(n N)的展开式中,前三项的系数依次成等差数列,则此展开式有理项的项数是 。
N)的展开式中,前三项的系数依次成等差数列,则此展开式有理项的项数是 。  B.
B. C.2
C.2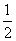
 的解集为
的解集为 ,则
,则 的解集为(
的解集为( )
) B.
B. C.
C. D.
D. 
 B.
B.
 D.
D. 
 ≥1,命题q∶
≥1,命题q∶ ≥
≥ 是
是 的 ( )
的 ( )